Review questions and answers
| Home | | Pharmaceutical Drugs and Dosage | | Pharmaceutical Industrial Management |Chapter: Pharmaceutical Drugs and Dosage: Biopharmaceutical considerations
Pharmaceutical Drugs and Dosage: Biopharmaceutical considerations - Review questions and answers
Review questions
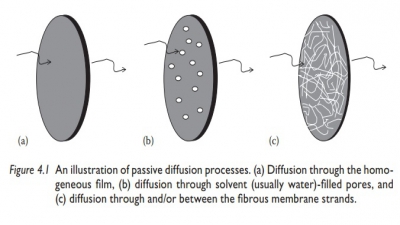
4.1 The characteristics
of an active transport process include all the fol-lowing, except:
A. Active transport
moves drug molecules against a concentration gradient.
B. It follows Fick’s
law of diffusion.
C. It is a
carrier-mediated transport system.
D. It requires energy.
E. Active transport of
drug molecules may be saturated at high drug concentrations.
4.2 The
passage of drug molecules from a region of high drug concentra-tion to the
region of low drug concentration is known as:
A. Active transport
B. Simple diffusion or
passive transport
C. Pinocytosis
D. Bioavailability
E. Biopharmaceutics
4.3 Which of
the following is true about Fick’s first law of diffusion?
A. It refers to a
nonsteady-state flow.
B. The amount of
material flowing through a unit cross-section of a barrier in unit time is
known as the concentration gradient.
C. Flux of material is
proportional to the concentration gradient.
D. Diffusion occurs in
the direction of increasing concentration.
E. All of the above.
4.4 Which
equation describes the rate of drug dissolution from a tablet?
A. Fick’s law
B. Henderson–Hasselbalch
equation
C. Michaelis–Menten
equation
D. Noyes–Whitney
equation
E. All of the above
4.5 The
diffusion coefficient of a permeant depends on:
A. Diffusion medium
B. Diffusion length
C. Temperature
D. All of the above
4.6 The rate of drug
dissolution from a tablet dosage form will increase with:
A. The particle size of
the drug
B. The surface area of
drug particles
C. The disintegration
time
D. The amount of
excipients to dilute the drug
4.7 The
permeability coefficient of a weak electrolyte through a biological membrane will increase
if:
A. The particle size of
the drug increases.
B. The surface area of
drug particles increases.
C. The partition
coefficient increases.
D. The drug dissolution
rate increases.
4.8 Indicate
which statement is true and which is false.
A. Fick’s first law of
diffusion states that the amount of material flowing through a unit
cross-section of a barrier in unit time is proportional to the concentration
gradient.
B. The diffusion rate
of molecules with a larger particle size is less than that of those with a
smaller particle size.
C. Under the sink
condition, the drug concentration in the receptor compartment is lower than
that in the donor compartment.
4.9 Define Fick’s first
law of diffusion. Describe how Fick’s first law is expressed in the
Noyes–Whitney equation for dissolution. Calculate the diffusion coefficient of
the new diet drug Lipidease® across a diffu-sion cell, given the following
information: mass rate of diffusion = 5 × 10–4 g/s, cross-section of
barrier = 1.0 cm2, and concentration gradi-ent = –175 g/cm4.
4.10 Calculate
the rate of dissolution (dM/dt) of
drug particles with a sur-face area of 2.5 × 103 cm3 and
a saturated solubility of 0.35 mg/mL at room temperature. The diffusion
coefficient is 1.75 × 10–7 cm2/s, and the thickness of
the diffusion layer is 1.25 μm. The drug concentra-tion in the bulk solution
is 2.1 × 10–4 mg/mL.
4.11 The diffusion
coefficient of tetracycline in a hydroxyethyl methacrylate—methyl methacrylate
copolymer film is D = 8.0 (±4.7) × 10–9
cm2/s and the partition coefficient, k, for tetracycline between the membrane and the reservoir is 6.8
(±5.9) × 10–3. The membrane thickness, h, of the trilaminar device is 1.40 × 10–2 cm, and the
con-centration of tetracycline in the concentration, C0, is 0.02 g/cm3 of the core material.
Calculate the release rate, Q/t, in
units of mg/cm2 of tetracycline per day.
4.12 Drug A
weighs 0.5 g and has a total surface area of 0.3 m2. In an experiment, it was found
that 0.15 g of A (C) dissolved in
1000 mL of water in the first 2 min. Sink conditions were present. The
saturation solubility was found to be 1.2 × 10–3 g/cm3.
Calculate the dissolution rate constant in cm/min. Assume that saturation
solubility, Csat, is much
greater than the value C.
Answers:
4.1 B.
4.2 B. In
passive transport, a drug travels from high concentration to a low
concentration, whereas active transport moves drug molecules against a
concentration gradient and requires energy.
4.3 C. Fick’s
first law of diffusion states that the amount of material flow through a unit
cross section of a barrier in unit time, which is known as the flux, is
proportional to the concentration gradient. Fick’s first law of diffusion
describes the diffusion process under steady-state conditions when the
concentration gradient does not change with time.
4.4 D. The
Noyes–Whitney equation describes the rate of drug dissolution from a tablet.
Fick’s first law of diffusion is similar to the Noyes–Whitney equation in that
both equations describe drug movement due to a concentration gradient. The
Michaelis–Menten equation involves enzyme kinetics, whereas
Henderson–Hasselbalch equations are used for determination of pH of the buffer
and the extent of ionization of a drug molecule.
4.5 D. Diffusion
coefficient is not a constant. It is affected by changes in the concentration,
temperature, pressure, solvent properties, and chemical nature of the
diffusant.
4.6 B. According
to the Noyes–Whitney equation, the rate of drug dissolution from a solid dosage
form will increase with increase in surface area, which will increase with
decrease in particle size or molecular weight of a drug.
4.7 C. The
permeability of a weak electrolyte through a biological mem- brane depends on
the degree of its ionization; the more lipophilic drug will permeate more,
which is possible when its partition coefficient increases.
4.8 A. True
B . True
C. True
4.9 Fick’s
first law of diffusion states that the amount of material (M) flowing through a
unit cross section (S) of a barrier in unit time (t) is proportional to the
concentration gradient (dC/dx).
J= 1/S dM/dt
= − D dC/dx = D(C1 − C2) / h
Because K = C1/Cd = C2/Cr,
we can rewrite this equation as
dM/ dt = DSK(Cd − Cr) / h = DSKCd / h
The rate at which a solid dissolves in a solvent can be determined
using the
Noyes–Whitney equation:
dM/ dt = kS(Cs − C)
Under sink conditions, when the drug concentration (C) is much
less than the solubility of the drug (Cs), we can ignore C (C → 0). A
sim-plified Noyes– Whitney equation can be used to measure dissolution rates:
dM/ dt = KSCs = DSCs/h
or
dC/dt = kSCs / V = DSCs
/ Vh
dM/ dt = DS(Cd − Cr) / h
D = 5× (10−4/175) ×1
D = 2 . 86 ×10−6 cm2 /s
4.10 dM / d t = S × D × (C1 − C2)/h, dM/
dt = (2 .5 ×103 ) × (1 . 75 ×10−7 ) × (0 .35 − 2.1 ×10−4 )/(1 .25 × 10 −4) = 1.225mg/s
4.11 Q/t = kDC0/h = (6 .8× 10−3 )(8 ×10−9 cm2 /s)
(0 .02 g/cm3 )/(1.40 ×10−2 cm) = 7 .77 ×10−11 gcm −2 s−1
To
obtain the results in micrograms per day, one must multiply the result by 106 μg/g and 86,400 s/24 h day.
Q/t = (7 .77 ×10 −11) gcm−2 s −1(106 µg/g)(86, 400 s/day)
=
6 .71 µg/cm2day
4.12 Cs >> C,
dM/dt = kS(Cs − C) = kSCs
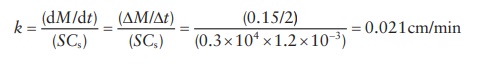
Related Topics