Concentration calculations

Concentration calculations

A formulation is essentially a multicomponent mixture. The relative amount of a substance in a multicomponent system represents its concentration. It could be the concentration of a dissolved drug in a solution, a suspended drug in a suspension, or a drug powder in a triturate of solid powders. The expression of concentration, its relation to the total amounts, and calculations involving changes to the concentration or total amount are an essential part of pharmacy practice. This section discusses the common ways of expressing concentrations, their basic principles, and the calcula-tions involving drug amounts in such preparations.

Percentage solutions

Concentrations of ingredients in a formula are often represented as a percentage (%). Percentage represents parts of 100 (cent). In liquid prepara-tions, percentage values can represent % weight/weight (% w/w, e.g., 2 g of solid in a 100 g of liquid = 2% w/w), % weight/volume (% w/v, e.g., 2 g of solid in 100 mL of liquid = 2% w/v), or % volume/volume (% v/v, e.g., 2 mL of liquid A in 100 mL of liquid B = 2% v/v of liquid A).

Calculations for the exact amount of an ingredient to be used in a for-mulation when the percentage composition of the formula is known can be made using ratio and proportion. Thus, to dispense 240 mL of a 10% w/v solution of a drug substance, the amount of drug substance needed can be calculated as:

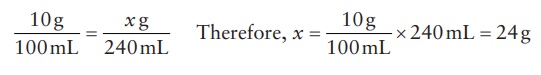
Concentrations based on moles and equivalents

Molecular weights or moles of a compound are more useful for calculations when two or more chemical compounds are to be compared for a given attribute. Thus, during drug discovery, relative potencies of different com-pounds are compared on a molar basis.

The concepts of solution concentrations of compounds are based on their molecular or equivalent weights, which can be defined as follows:

·           The molecular weight of a compound represents the weight of one mole (abbreviation: mol) of a compound, in grams. Thus, 1 mole of glucose is 180.16 g of glucose. The molar mass of glucose is thus represented as 180.16 g/mol.

·           An equivalent weight of a compound represents its molecular weight divided by the number of valence or ionic charges in solution. It takes into account the chemical activity of an electrolyte. One equivalent (abbreviation: Eq), in grams, of a compound represents 1 mole of compound in grams divided by its valence. Thus, molecular weight of Mg²⁺ ions is 24.3 g, indicating that 24.3 g of Mg²⁺ ions represents 1 mole of Mg²⁺. On the other hand, the equivalent weight of Mg²⁺ ions is 24.3/2 = 12.15 g, since there are two charges on Mg²⁺ ions. Thus, when used for charge-neutralization calculations, 1 mole or molecular weight of Mg²⁺ ions represents two equivalents.

Solutions of electrolytes are often prepared in terms of molarity, molality, and normality.

·           Molarity (abbreviation: M) is defined as the moles of solute per liter of solution. Therefore, 1 M of sulfuric acid solution represents 98 g (molecular weight) of H₂SO₄ dissolved in 1 L of solution.

·           Normality (abbreviation: N) represents gram equivalent weight of solute per liter of solution. The difference between molarity and normality is representative of the difference between moles and equiv-alents of a compound. Thus, 1 N of sulfuric acid solution represents 49 g (equivalent weight) of H₂SO ₄ dissolved in 1 L of solution. The equivalent weight of H₂SO₄ is half its molecular weight, since H₂SO₄ is a diprotic acid (i.e., dissociates to release 2 H⁺ ions in solution).

·           Molality (abbreviation: m) is a less frequently used term that represents the number of moles of solute per kilogram of solvent.

·           Formality (abbreviation: F) is another less frequently used term that represents the formula weight of a compound in 1 L of solution. It differs from molarity in indicating the amount of solute added to the solution, but it does not consider the nature of the chemical species that actually exist in solution. For example, when 1 mole of sodium carbonate (Na₂CO₃) or sodium bicarbonate (NaHCO₃) is dissolved in a total of 1 L of an acidic solution of hydrochloric acid (HCl), the concentration of Na₂CO₃ or NaHCO₃ may be represented as 1 F (indicates the amount added) but not as 1 M (indicates amount in solution)—even though quantitatively they would be the same—since the compound reacts with acid in the solution and does not remain as the same species that was added.

·           The amount of a solute may also be represented as its mole fraction. The mole fraction of a solute is the number of moles of solute as a proportion of the total number of moles (of solute + solvent) in a solu-tion. For example, a mole fraction of 0.2 indicates 2 moles of solute dissolved in 8 moles of solvent. Mole fraction is a dimensionless quan-tity. Mole fraction is frequently used to represent the relative amount of two different solutes in a system.

Concentrations and amounts can be represented in fractions by using the prefixes used in the metric system of measure. Thus, 1 mEq is one milliequivalent of a solute, thus representing 1/1,000th of an equivalent weight of the solute. Similarly, 1 μM would represent 1 micromolar, or 1/1,000,000th of a molar (1 mol/L) concentration of a solute.

Parts per unit concentrations

Parts per unit concentrations are commonly expressed for very low con-centrations of solutes. The commonly used parts per unit concentrations are as follows:

·           Parts per million (ppm) represents 1 part of a substance in 1 million (10⁶) parts of the total mixture. Parts per million (ppm) is dimension-less, since the parts of both the substance and the total mixture are represented in the same units. In addition, this measure is applicable to both solutions and solids. Thus, 1 ppm of NaCl in a solid powder may represent 1 μg/g or 1 mg/kg of NaCl. Moreover, 1 ppm of NaCl solution can represent 1 μL/L of NaCl in water.

·           Parts per billion (ppb) represents 1 part of a substance in 1 billion (10⁹) parts of the total mixture. Similar to ppm, it is dimensionless and does not represent a state (solid or liquid) of the substance.

·           Other less commonly used parts per unit measures are parts per thousand, parts per trillion (ppt, 1 in 10¹²), and parts per quadrillion (ppq, 1 in 10¹⁵).

Dilution of stock solutions

A stock solution is a concentrated solution of a substance that can be diluted to a lower, desired concentration by adding the solvent immediately before use or dispensing. Stock solutions are frequently used in pharmacy dispensing to increase the efficiency, ease, and accuracy of dispensing, as well as the space and cost advantages with the transportation and storage of lower-volume concentrated solutions.

A common calculation required for the dilution of a concentrated stock solution to a desired concentration is the amount of solvent needed to achieve the desired concentration. This can be derived from the formula for concentration (c) based on the volume (v) of solution and the weight (w) of the substance.

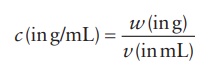
Therefore, if the stock solution were designated by the subscript “1” and the final solution to be prepared by the subscript “2,”

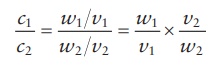
Since it is the same weight of the solute that would be transferred from the stock solution into the final, diluted solution,

w₁ = w₂

Therefore,

c₁ × v₁ = c ₂ × v₂                     (5.3)

This formula can be used to calculate the volume of solvent required to make a diluted solution. For example, to dilute a 50% w/v stock solution to make 200 mL of a 5% w/v solution, c₁ = 50, c ₂ = 5, and v₂ = 200.

v₁ = ( c₂ × v₂ ) / c₁ = ( 5 × 200 ) / 50 = 20mL

Hence, the amount of stock solution needed = 20 mL and the amount of solvent needed = 200 − 20 = 180 mL to make a total of 200 mL of the diluted solution.

The measurements can also be carried out in weight rather than in vol-ume for the stock and the diluted solutions. Thus,

c₁ × w₁ = c ₂ × w₂                        (5.4)

Mixing solutions of different concentrations

Often, mixing of two products made of the same solute but having different concentrations is required. A convenient approach to solve these problems is the alligation method. Two kinds of alligation methods are commonly used: alligation medial and alligation alternate.

Alligation medial

For two ingredients

This method is based on finding the proportion for a formula. The strength (e.g., % w/w) of an ingredient is multiplied by its amount (e.g., quantity in grams) to obtain the product of each ingredient. The products of all ingre-dients and their quantities in the original formula are added together sepa-rately. Dividing the sum of products by the sum of quantities in the original formula gives a quotient, which represents the strength (e.g., % w/w) of the final mixture.

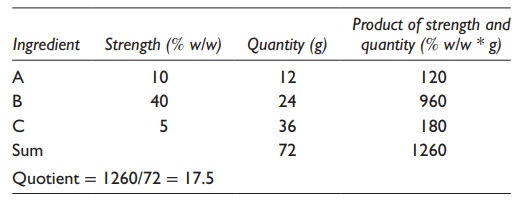
For example, to calculate the strength of the final mixture when 12 g of a 10% w/v sucrose solution is mixed with 24 g of a 40% w/v sucrose solution, one would write the alligation medial method as indicated in Table 5.1. Working through this table, the final solution would be of 30.0% w/w strength.

For more than two ingredients

This method is also applicable for more than two ingredients. For example, to calculate the strength of the final mixture when 12 g of a 10% w/v sucrose solution is mixed with 24 g of a 40% w/v and 36 g of a 5% w/v sucrose solu-tion, one would write the alligation medial method as indicated in Table 5.2. Working through this table, the final solution would be of 17.5% w/w strength.

Table 5.1 Alligation medial method for two ingredients

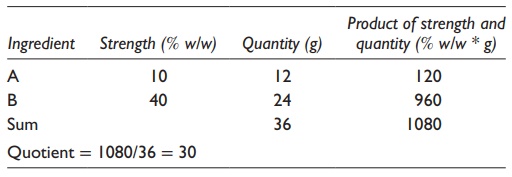
Table 5.2 Alligation medial method for more than two ingredients

Alligation alternate

For two ingredients

This method can be used to calculate the amount of a diluent, solute, or different-concentration product that would need to be added to a given concentration product to make a new concentration preparation. The num-ber of parts required for the lower- and higher-concentration preparations to make the target-concentration preparation is obtained by constructing a matrix and doing the calculation as shown in Table 5.3.

Table 5.3 Alligation alternate method for two ingredients

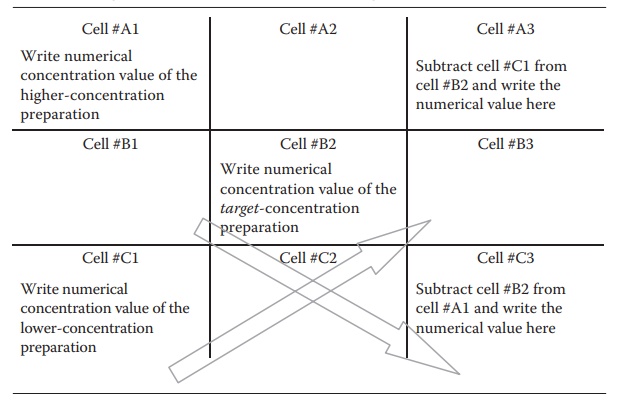
Thus, subtracting the target concentration from the lower concentration gives the target amount of the higher-concentration preparation, and subtracting the higher concentration from the target concentration gives the target amount of the lower-concentration preparation.

Thus, the total amount of the target-concentration preparation that would be prepared can be obtained by adding together the target amounts of higher- and lower-concentration preparations needed. If the required amount of the target-concentration preparation is dif-ferent than the amount obtained by the formula, the principles of propor-tion, discussed earlier, can be used to calculate the quantities needed for the required total amount of the target-concentration preparation.

For example, to prepare 200 mL of a 12% w/v sucrose solution using a 40% w/v and another 5% w/v sucrose solution, one would write the alligation matrix as shown in Table 5.4.

Thus, combining 7 mL of 40% w/v solution with 28 mL of 5% w/v solution would give 7 + 28 = 35 mL of 12% w/v solution. To make 200 mL of 12% w/v solution, one would use the principles of proportion as follows:

For the quantity of 40% w/v solution,

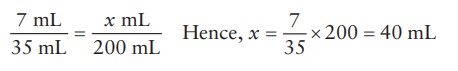
For the quantity of 5% w/v solution,

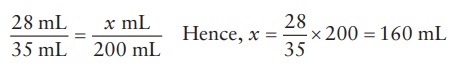
Alternatively, a conversion factor could be derived for the calculation:

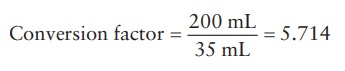
The required quantities of low- and high-concentration solutions can then simply be obtained by multiplying their quantities obtained by the alliga-tion formula by this factor. Thus, the quantity of 40% w/v solution required = 7 × 5.714 = 39.998 = 40 mL. Therefore, the quantity of the 5% w/v solution required = 200 − 40 = 160 mL or 28 × 5.714 = 159.992 = 160 mL.

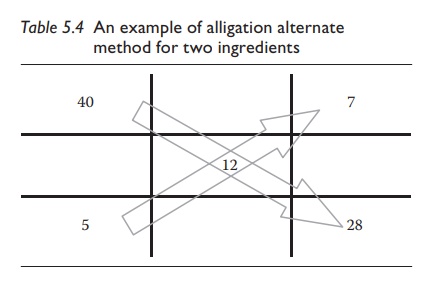
Table 5.5 An example of alligation alternate method for more than two ingredients

For more than two ingredients

The alligation alternate method can be used for more than two ingredients by pairing off the values of one higher (than the desired) strength ingredient with two lower (than the desired) strength ingredients, or vice versa. This is illustrated by the following example:

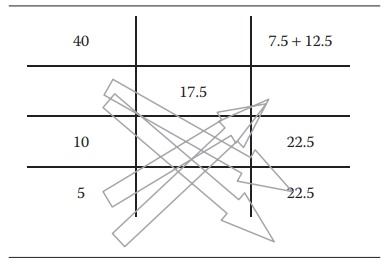
To prepare a 17.5% w/w solution using a 10% w/v, a 40% w/v, and a 5% w/v sucrose solution, one would write the alligation alternate method, as shown in Table 5.5.

Thus, combining 20 mL of 40% w/v solution with 22.5 mL of 10% w/v solution and 22.5 mL of a 5% w/w solution would give 20 + 22.5 + 22.5 = 65 mL of 17.5% w/v solution. The laws of proportion can be used, as described earlier, to calculate specific quantities of starting solutions that would be needed to prepare a desired quantity of the final solution.

The alligation alternate method for more than two ingredients can use any pairing of higher (than the desired) strength ingredient(s) with lower (than the desired) strength ingredient(s). The pairings can be any number depending on the number of ingredients.

The alligation methods are applicable to all forms of preparations, including powders. In addition, the alligation method can also be used for calculating the required quantities for dilution of a preparation with the solvent or diluent alone by making the concentration of the lower-concentration preparation zero.

Tonicity, osmolarity, and preparation of isotonic solutions

Of the two compartments of solution separated by a semipermeable membrane, the solvent tends to flow from the solution with the lower solute concentration to the solution with the higher solute concentration. If uninterrupted flow of solvent is allowed, it would result in the equaliza-tion of concentration across the membrane. This phenomenon is called osmosis. The pressure of solvent involved in this phenomenon is termed  osmotic pressure. A solution containing a nonpermeable solute creates a pressure for the inward flow of solvent across the semipermeable mem-brane. Thus, osmotic pressure can also be defined as the pressure that must be applied to a solution to prevent the inward flow of solvent across a semipermeable membrane.

Tonicity is the osmotic pressure of two solutions separated by a semiper-meable membrane. Tonicities of solutions are often represented with refer-ence to that of normal body fluids. Thus, solutions that exert lower osmotic pressure than the body fluids are termed hypotonic, while solutions that exert higher osmotic pressure than the body fluids are termed hypertonic. Hypotonic solutions have lower and hypertonic solutions have higher impermeable solute concentration than the body fluids. Two solutions that have the same osmotic pressure are termed isosmotic, while a solution that has the same osmotic pressure as a reference body fluid is termed isotonic.

To define the osmotic amount and concentration of a solute without referring to another solution, the concepts of osmole, osmolarity, and osmolality are introduced. An osmole is the amount of a substance that represents the number of moles of particles that it forms in a solution. For a nondissociating substance, that is, a nonelectrolyte such as dextrose, 1 osmole = 1 mole. Thus, 1 osmole of dextrose = 186 g (molecular weight) of dextrose.

Similar to the concept of molarity, osmolarity (abbreviation: Osmol) is defined as the osmoles of solute per liter of solution. Therefore, 1 Osmol of glucose solution represents 186 g (molecular weight) of glucose dissolved in 1 L of solution.Similar to the concept of molality, osmolality is defined as the osmoles of solute per kg of solvent. These quantities can be used with prefixes in the metric system, such as milli and micro. Thus, a commonly used term is milliosmole (abbreviation: mOsmol), which represents 1/1,000th of an Osmol. Moreover, while osmole represents the quantity of solute in grams, Osmol represents the concentration of solute in a solution.

For a dissociating solute, such as an electrolyte, 1 mole ≠ 1 Osmol and 1 M solution ≠ 1 Osmol solution. The osmoles and osmolarity of such a solute are calculated by multiplying with the number of particles formed on dissociation and the fractional degree of dissociation of a substance in solution. Thus, assuming complete dissociation, NaCl, CaCl₂, and FeCl₃ form 2, 3, and 4 particles in solution. Thus, 1 mM solution of NaCl, CaCl₂, or FeCl₃ represents their 2, 3, or 4 mOsmol solution, respectively. Assuming, 80% degree of dissociation for dilute solutions, 2 M of NaCl, CaCl₂, and FeCl₃ solutions represent:

2 × (1 + 80/100) = 3.6 Osmol of NaCl solution

2 × (1 + 80/100 + 80/100 ) = 5.2 Osmol of CaCl₂ solution

2 × (1 + 80/100 + 80/100 + 80/100 ) = 6.8 Osmol of FeCl₃ solution

The normal serum osmolality is in the range of 275–300 mOsmol/kg. osmolality of solutions can be measured in the laboratory by using an osmometer.

Tonicity is an important concept in the administration of ophthalmic and parenteral solutions. Hypertonic solutions tend to draw fluids out of body tissues, leading to irritation and dehydration. Hypotonic solu-tions, on the other hand, can provide excess fluid to the body tissues. However, since the volume of the administered solution is much lower than that of body fluids and fluid elimination is a regulated physiological phenomenon, hypotonic solutions are relatively inconsequential. Thus, administration of hypertonic solutions tends to be more tissue-damaging and painful than the administration of hypotonic solutions. Nonetheless, isotonic solutions are better tolerated by patients than either extremes of tonicity.

Preparation of isotonic solutions requires the use of one of the col-ligative properties of solutions. Colligative properties are the solution properties that depend on the number of molecules of solvent in a given volume of solution but are independent of the properties of the solute. These properties include lowering of vapor pressure, elevation of boiling point, osmotic pressure, and depression of freezing point of a solution with increasing solute concentration. Of these, the depression of freezing point is conveniently used to calculate the amount of solute required to prepare an isotonic solution.

For example, given that the freezing point of blood serum and ophthalmic lachrymal fluid is −0.52°C and that 1 M aqueous solution of a nonelectro-lyte depresses the freezing point of water by 1.86°C, we can calculate the amount of glucose (molecular weight: 180 g/mol) required to prepare an isotonic solution by solving for the amount of glucose that would produce a freezing point depression of 0.52°C. Thus, to make 1 L of isotonic glucose solution, the amount of glucose required (x) can be calculated as:

This corresponds to 5% w/v glucose solution. The commonly available dextrose solution for intravenous (IV) administration has this concentra-tion. Similar concentration for an electrolyte, such as sodium chloride, should take into consideration the dissociation constant of the solute and the number of species produced in the solution. Thus, assuming that NaCl in weak solutions is about 80% dissociated, the total number of solutes in solution would be 1.8 times the number of molecules added to the solution. This (1.8) dissociation factor (abbreviation: i) is used in the calculation of isotonic concentrations of electrolytes. Thus, to make a 1 L isotonic NaCl (molecular weight: 58 g/m) solution, the amount of NaCl required (x) can be calculated as:

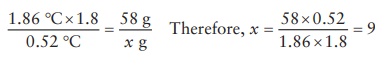
This corresponds to 0.9% w/v NaCl solution, which is commonly available as an isotonic solution for experiments involving living cell and tissues. From these calculations, note that 50 g/L of glucose solution is isotonic to 9 g/L of NaCl solution. Therefore, in quantities of solutes, 50 g of glucose is tonic equivalent to 9 g of NaCl. The tonic equivalence of two substances represents their amounts that would produce the same osmotic pressure. Thus, the quantity of any substance divided by its dissociation factor, i, represents its tonic equivalent quantity to any other substance. This principle is used in the preparation of isotonic solutions by the addi-tion of NaCl to hypotonic drug solutions to increase the tonicity to the physiological equivalent of 0.9% w/v NaCl. Using the above conversion of tonic equivalents, NaCl equivalents (E values) of various substances are known in the literature. The number of grams of all ingredients in a pre-scription is multiplied by their E values and added together to determine the osmotic equivalent of NaCl amount represented by the substances. In addition, the amount of NaCl that would be required to make a 0.9% w/v solution of the same volume as the prescription is determined. Subtracting the former from the latter gives the amount of NaCl needed to make the solution isotonic. Any substance other than NaCl, such as dextrose, can also be used to increase the tonicity of a solution by dividing the amount of NaCl needed by the NaCl equivalent of the other substance.

For example, to compound 10 mL of an ophthalmic preparation of 3% w/v pilocarpine nitrate, we first determine the amount of drug in 10 mL of solution.

Drug amount = 3/100 ×10 = 0 .3 g

The NaCl equivalent (E value) of pilocarpine nitrate (molecular weight 271, dissociates into 2 ions, and i value = 1.8) can be read from the literature or calculated as:

E value = (58. 5 / 1.8) / (271 / 1.8) = 0.216

Now, we multiply the E value with the drug amount in solution to get NaCl equivalents represented by the drug amount in the solution:

NaCl equivalent in prescription = 0.3× 0.216 = 0.0648 g

This is the amount of particles in solution equivalent to NaCl, which must be subtracted from the amount of NaCl that would be needed to make an isotonic solution of the same volume as the prescription (i.e., 10 mL). This is calculated as:

Total amount of NaCl needed for isotonicity = (0.9/100) × 10 = 0 .09 g

Hence, the amount of NaCl that must be added to the prescription to make an isotonic solution = 0.09−0.0648 = 0.0252 g.

If a prescription contains multiple components, NaCl equivalent for each component is calculated separately and added together to make the total NaCl equivalents in the prescription. This total amount is then subtracted from the total NaCl that would be needed for isotonicity of the volume of pre-scription to obtain the amount of NaCl that must be added to the prescription.