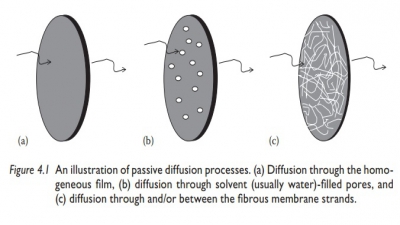
Diffusion rate

Diffusion rate

Fick’s first law of diffusion describes the diffusion process under steady state when the concentration gradient (dC/dx) does not change with time. The second law refers to a change in the concentration of diffusant with time at any distance (i.e., a nonsteady state). Diffusive transport from a dosage form is usually slow, leading to most of the drug transport happen-ing under steady-state conditions. Therefore, it is important to understand the diffusive conditions under a steady state.

Diffusion cell

Figure 4.2 shows the schematic of a diffusion cell, with a diaphragm of thickness h and cross-sectional area S separating the two compartments. A concentrated solution of drug is loaded in the donor compartment and allowed to diffuse into the solvent in the receptor compartment. The solvent in both the compartments is continuously mixed and sampled frequently to quantitate drug transport across the membrane.

Equating both equations for flux, Fick’s first law of diffusion may be written as:

in which (C₁ − C₂)/h approximates dC /dx. Concentrations C₁ and C₂ within the membrane (Figure 4.2) are determined by the partition coefficient of the solute (K_{membrane/solvent}) multiplied by the concentration in the donor com-partment (C_donor) or in the receptor compartment (C_receptor). Thus, we have:

C1 = C_donor × K_{membrane solvent} (4.8)

and

C₂ = C_receptor × K_{membrane solvent} (4.9)

Therefore, the partition coefficient is given by:

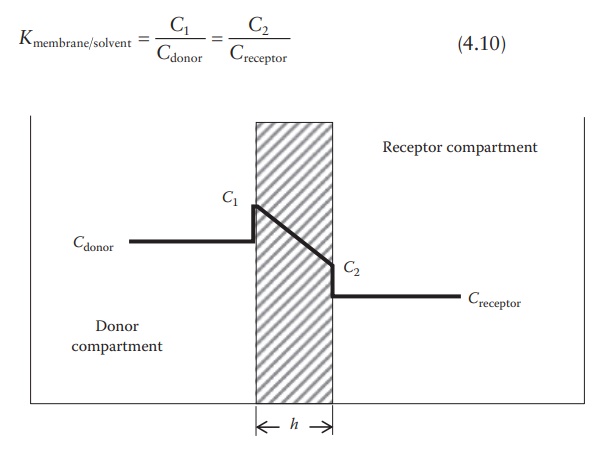
Figure 4.2 Drug concentrations in a diffusion cell.

Hence,

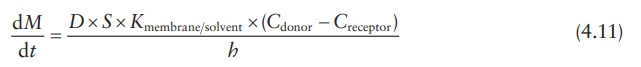
Under sink conditions, the drug concentration in the receptor compart-ment is maintained much lower than the drug concentration in the donor compartment, such that C_receptor → 0. Therefore, the above equation can be simplified as:

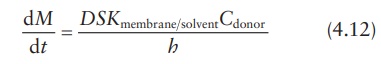
This equation can also be expressed in terms of the permeability coeffi-cient, P, in cm/s, which is defined as:

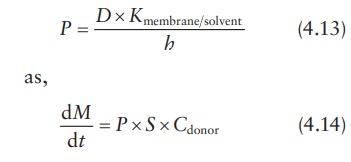
Spherical membrane-controlled drug delivery system

Following the same principles as outlined above for a diffusion cell, dif-fusive drug release from a spherical rate-limiting membrane enclosing a drug solution can be defined in terms of the surface area of the membrane at the center point of its thickness and the linear distance of drug diffusion across the membrane, x. Given the inner-boundary radius of the membrane as r_inner and the outer-boundary radius of the membrane as r_outer, the surface area of the sphere at its mean radius is given by:

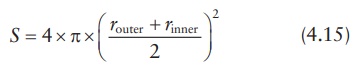
The surface area of the sphere may be approximated by:

S = 4 × π × r_outer × r_inner (4.16)

And the linear distance for solute diffusion across the membrane is given by:

x = r_outer – r_inner (4.17)

Thus, the expression for the drug-release rate from a sphere is:

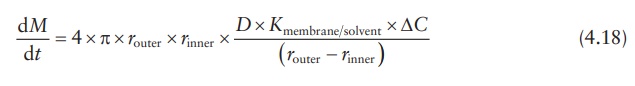
where ΔC is the concentration gradient between the inside and the outside of the membrane.

Thus, permeability depends on both the properties of the diffusing solute (partition coefficient and diffusion coefficient) and the properties of the membrane (thickness and surface area).

Pore diffusion

In microporous reservoir systems, drug molecules are released by diffusion through the solvent-filled micropores. Drug transport across such porous membranes is termed pore diffusion. In this system, the pathway of drug transport is no longer straight but tortuous. The rate of drug transport is directly proportional to the porosity, ε, of the membrane and inversely pro-portional to the tortuosity, τ, of the pores. In addition, the partition coef-ficient of the drug between the membrane and the solvent (K_{membrane solvent}) is no longer a factor, since drug dissolution in the membrane is not required. Therefore,

In this modified equation, D_s is the drug diffusion coefficient in the solvent.

Determining permeability coefficient

Using the permeability coefficient:

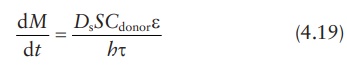
where, surface area is given by:

S = 4 × π × r_outer × r_inner                  (4.16)

and concentration gradient is given by ΔC = C_donor − C_receptor, with the assumption that C_receptor → 0 under sink conditions; thus, if ΔC ≅ C_donor , we obtain:

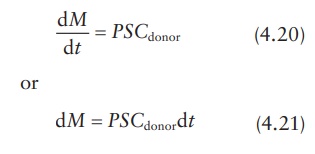
Thus, the value of permeability coefficient, P, can be obtained from the slope of a linear plot of M versus t, provided that C_donor remains relatively constant.

Lag time in non-steady state diffusion

sustained-release dosage form may not exhibit a steady-state phenom-enon from the initial time of drug release. For example, the rate of drug diffusion across a membrane slowly increases to steady-state kinetics (Figure 4.3). As shown in this figure, the curve is convex to the time axis in the early stage and then becomes linear. This early stage is the nonsteady-state condition. Later, the rate of diffusion is constant, the curve is essen-tially linear, and the system is at a steady state. When the steady state portion of the line is extrapolated to the time axis, the point of intersection represents the time of zero diffusion concentration if the system had been at the steady state all along. This time period between the actual nonsteady state and the projected steady-state time at zero diffusion concentration is known as the lag time. This is the time required for a penetrant to establish a uniform concentration gradient within the membrane that separates the donor from the receptor compartments.

Matrix (monolithic)-type non-degradable system

In a matrix-type polymeric delivery system, the drug is distributed through-out a polymeric matrix. The drug may be dissolved or suspended in the polymer. Regardless of a drug’s physical state in the polymeric matrix, the release of the drug decreases over time. 

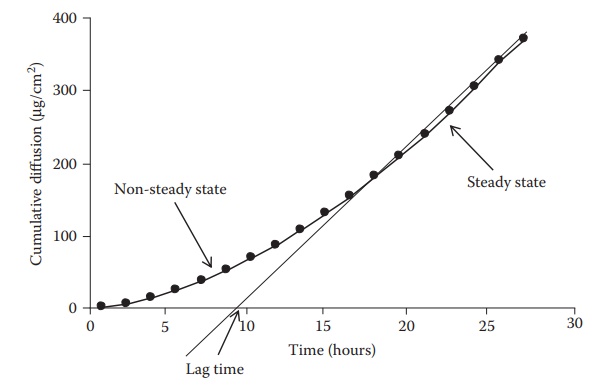
Figure 4.3 Drug diffusion rate across a polymeric membrane.

In these systems, drug molecules can elute out of the matrix only by dissolution in the surrounding poly-mer (if drug is suspended) and by diffusion through the polymer structure. Initially, drug molecules closest to the surface are released from the device. As drug release continues, molecules must travel a greater distance to reach the exterior of the device. This increases the diffusion time required for drug-release. This increase in diffusion time results in a decrease in the drug-release rate from the device with time.

In an insoluble matrix-type system, the drug-release rate decreases over time as a function of the square root of time (Higuchi, 1963).

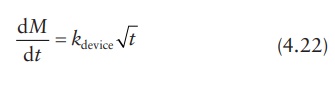
where k_device is a proportionality constant dependent on the properties of the device.

This release kinetics is observed for the release of the first 50%–60% of the total drug content. Thereafter, the release rate usually declines expo-nentially. Thus, the reservoir system can provide constant release with time (zero-order release kinetics), whereas a matrix system provides decreasing release with time (square root of time-release kinetics).

Calculation examples

Drug-release rate

Calculation of diffusion coefficient across and partition coefficient into a membrane barrier of a drug delivery system is often undertaken to simulate drug-release rate kinetics under different formulation conditions, such as drug loading. The diffusion rate may be calculated by using experimental data in one set of experiments. For example, if it were known that the diffusion coefficient of tetracycline in a hydroxyethyl methacrylate–methyl methacrylate copolymer film is D = 8.0(±4.7) × 10^–9 cm²/s and the partition coefficient, K, for tetracycline between the membrane and the reservoir fluid of the drug delivery device is 6.8(±5.9) × 10^–3, drug-release rate can be calculated if the design parameters of the device are known. If the mem-brane thickness, h, of the device is 1.4 × 10^–2 cm and the concentration of tetracycline in the core, C_core, is 0.02 g/cm³, tetracycline-release rate, dM/dt, may be calculated as follows.

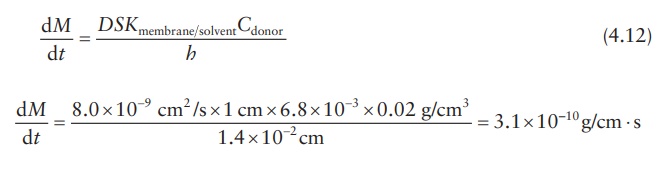
To obtain the results in micrograms per day,

dM / dt  = 3 . 1× 10⁻¹⁰ g/cm ⋅ s × 10⁶ µg/g × 60 × 60 × 24 s/day = 26.85 µg/day ⋅ cm

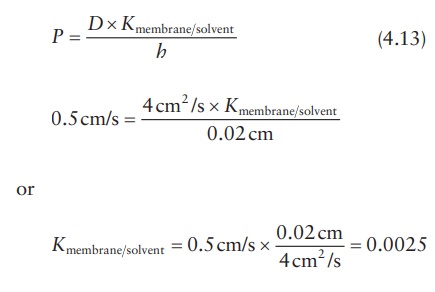
Partition coefficient

Knowing the permeability coefficient and the diffusion coefficient of a drug in a membrane, its partition coefficient can be calculated. For example, if a new glaucoma drug diffuses across a barrier of 0.02 cm with a permeability coefficient of 0.5 cm/s and the diffusion coefficient is 4 cm²/s, its perme-ability coefficient may be calculated as follows: