Strain in Ring Systems

STRAIN IN RING SYSTEMS

Molecules which contain rings comprise an important subset of organic com-pounds. In many respects their behavior and properties are identical to those of functionally analogous open-chain systems. In other respects, however, the greater structural order imposed by a ring causes the properties of cyclic com-pounds to be quite different than analogous open-chain systems. These differences arise from the need to accommodate preferred bond angles and conformations in structures which restrict the adoption of optimal geometries.

As we have seen previously, molecules with saturated carbon atoms have preferred bond angles of about 109^◦ around the carbons and they are found primarily in staggered, anti conformations. This geometry allows the optimal overlap of all the interacting orbitals and yields the greatest amount of bond energy to be gained. Consequently the molecule has a lower energy than any other geometry and is thus the most stable.

It is possible to measure the heats of combustion for a series of saturated hydrocarbons and thereby determine how much energy is released (− ΔH_comb) when a –CH₂–group in a saturated hydrocarbon reacts with oxygen. Thus the heat of combustion of an open-chain methylene group is −157.4 kcal/mol. (The heat of combustion is negative because heat is evolved.)

–CH₂– + 3/2 O₂ → CO₂ + H₂O         ∆Hcomb = −157.4 kcal/mol

By a similar method, the heats of combustion of methylene groups in various ring compounds can be determined and the results are presented in Table 6.2. These data show that only cyclohexane and rings larger than C₁₃ have methylene groups of the same energy as methylene groups in open-chain systems. Since in every case the products of combustion (1 CO₂ and 1 H₂O) are the same, any differences in the heats of combustion must reside in the methylene groups themselves. The value of 157.4 kcal/mol represents the least amount of energy that can be released by combustion since an open-chain methylene group is at the lowest energy possible for that unit. All other values are equal to or higher than 157.4 kcal/mol.

A value of − ΔH_comb/–CH₂–unit = 157.4 kcal/mol (as in cyclohexane) indi-cates that a methylene group in that compound is as stable as one in an open-chain system and thus it is at the lowest possible energy. A value of ΔH_comb/–CH₂–unit >157.4 mkcal/mol means that a methylene group in that ring system is less sta-ble and therefore of higher energy than a methylene group in an open-chain compound by an amount equal to the difference between its comb and 157.4 [Δ(ΔHcomb)]. These differences are shown in the third column of Table 6.2.

Finally, since each ring system contains a different number of methylene groups, the total increase in energy of the ring system due to all the methylene groups is found by multiplying the Δ(ΔH_comb) by the number of methylene groups in the molecule. This is shown in the last column as total strain.

Strain can be defined as an increase in energy of a molecule (making it less stable) which results from any structural feature which causes nonoptimal overlap of atomic orbitals. Imperfect overlap leads to weaker bonds so less energy is derived from bond formation. 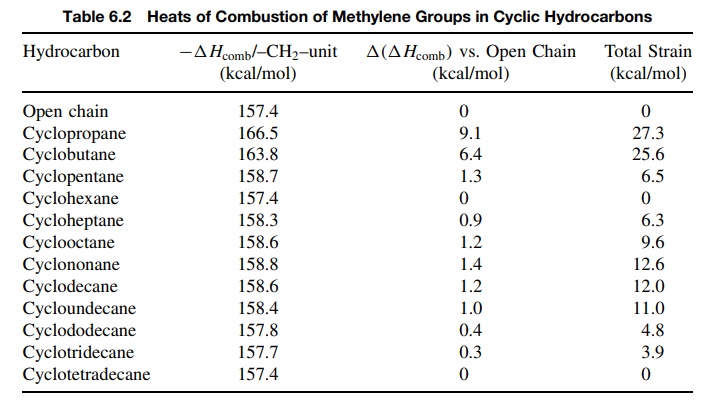Strain energy is the increase in energy due to imperfect overlap compared to the energy of an analogous system which has optimal overlap and the most bonding energy possible. This is shown for small rings in Figure 6.8.

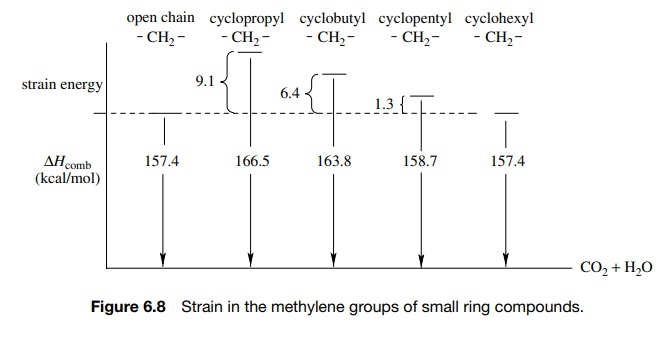
The methylene groups of cyclopropane are less stable by 9.1 kcal/mol than the methylene groups in open-chain hydrocarbons, and cyclopropane itself contains 27.3 kcal/mol of strain energy because there are three such methylene groups. Cyclopropane is a strained molecule because the three-membered ring requires that the bond angles at carbon be 60^◦ when saturated carbon normally has bond angles of 109^◦ . The distortion of bond angles from the normal tetrahedral geom-etry leads to increased energy or strain.

The smaller bond angles prevent normal overlap along the internuclear axis (dotted line). Overlap occurs outside the internuclear axis and a “bent” bond is formed (also referred to as a τ bond). The τ bond is weaker than a σ bond due to nonoptimal overlap and thus is of higher energy. This type of strain is termed angle strain (sometimes called Baeyer strain). It comes about because normal bond angles are not possible and thus nonoptimal overlap results. Angle strain in cyclopropane is manifested chemically by greater chemical reactivity of the τ bonds. 

Thus cyclopropane reacts with bromine, acids, and can be hydrogenated in stark contrast to an unstrained alkane, which is inert to these reagents.

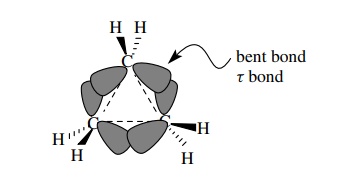
Cyclobutane also exhibits angle strain since 90^◦ bond angles are required by the four-membered ring instead of the preferred tetrahedral geometry. As expected, however, the amount of angle strain is less than in cyclopropane. The ring bonds of cyclobutane are still τ bonds, but they are closer to the internuclear axis and the overlap is better. Consequently they are more stable (stronger) than the τ bonds in cyclopropane. The greater bond strength is manifested by a lower chemical reactivity. Cyclobutane is more like an unstrained alkane and does not react with bromine or acids, although it can be hydrogenated under high pressure.

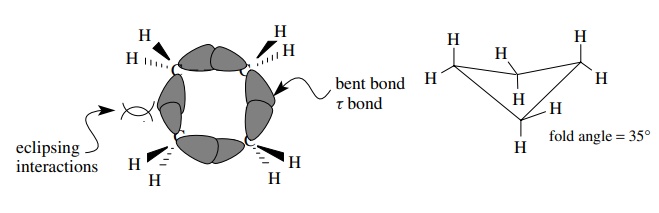
To achieve a bond angle of 90^◦ , cyclobutane must be planar. This would force the adjacent C–H bonds to be eclipsed and would also raise the energy of the system. As a compromise, cyclobutane folds diagonally by 35^◦ . While this raises the angle strain somewhat, it decreases the eclipsing interactions so that the lowest possible energy is attained. While each methylene group is less strained than one in cyclopropane, the total molecular strain is similar to that of cyclopropane.

If planar, cyclopentane should have minimal strain energy since the internal angles of a regular pentagon (108^◦ ) are very close to the normal tetrahedral angle. In fact, cyclopentane is a strained by 6.5 kcal/mol. If it were planar, all the hydrogen atoms around the cyclopentane ring would be eclipsed. This results in a second type of strain called torsional strain. Torsional strain is an increase in energy due to enforced eclipsing interactions. To reduce the torsional strain, cyclopentane adopts an “envelope” conformation in which one apex is bent out of the molecular plane by some 20^◦ . This introduces some angle strain but reduces the torsional strain and is the lowest energy structure that the molecule can achieve.

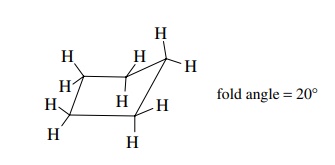
Any one of the five methylene groups of cyclopentane can be bent out of plane; thus cyclopentane is a dynamic system which undergoes a series of con-formational changes between different envelope conformations.

The methylene groups of cyclohexane have the same ΔH_comb as methylene groups in open-chain systems and thus cyclohexane is unstrained. It was orig-inally predicted by Baeyer that cyclohexane should have angle strain due to required bond angles of 120^◦ for a planar structure. In fact, cyclohexane adopts a puckered conformation in which all the bond angles are 109^◦ and all the hydrogens are perfectly staggered. The chair conformation of cyclohexane and its conformational ramifications have been discussed earlier.

It is also expected that rings larger than C₆ could adopt puckered structures and thus maintain normal bond angles and staggered groups. As such they should be unstrained. In fact, it is seen in Table 6.2 that ring systems between 7 and 13 members are all strained to some degree. This strain results from the fact that puckering causes some hydrogens across the ring to approach each other closer than the sum of their van der Waals radii. These transannular interactions cause an adjustment in the conformational structure and raises the energy of the ring system. This increase in energy seen in medium-sized rings (C₇ – C₁₃) is called transannular strain. After the ring size has reached C₁₄, the interior of the ring is large enough to minimize transannular strain. Consequently the ΔHcomb returns to the normal value of 157.4 kcal/mol found in unstrained systems.

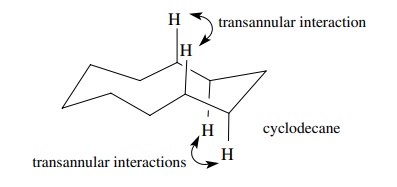
It must be emphasized that angle strain, torsional strain, and transannular strain are simply terms invented by chemists to categorize structural features in rings which lead to increased energy (strain). The molecules themselves adopt structures which are the most stable and have the greatest amount of bonding energy. Nevertheless, strain is an important feature in molecules to keep in mind since it is manifested by altered chemical reactivity.

For example, molecules which have significant angle strain such as cyclo-propanes, epoxides, and aziridines undergo ring cleavage reaction very readily. Such reactions are very exergic because the strain energy is released upon ring opening. The exergic nature of these ring-opening reactions means that they have early transition states and generally have low activation energies. Conversely the formation of small rings requires that the strain energy must be added to the products in order for them to form.

Medium rings are difficult to form by intramolecular ring-closing reactions because the transannular strain in the products increases the energy of the tran-sition state leading to those products. Thus the energy barrier to ring closure is raised and the intramolecular ring closure slows down significantly. Consequently intermolecular reactions (and not intramolecular ring-closing reactions) predom-inate. Transannular strain is not the only factor influencing these processes, but it is a major factor.

Saturated six-membered rings are easy to produce because they are unstrained. They are also resistant to ring-opening reactions for the same reason. Conse-quently saturated six-membered rings are the most common ring systems in the natural world.