Acidic and Basic Properties of Amino Acids
| Home | | Biochemistry |Chapter: Biochemistry : Amino Acids
Amino acids in aqueous solution contain weakly acidic α-carboxyl groups and weakly basic α-amino groups. In addition, each of the acidic and basic amino acids contains an ionizable group in its side chain.
ACIDIC AND BASIC PROPERTIES OF AMINO ACIDS
Amino acids in aqueous
solution contain weakly acidic α-carboxyl groups and weakly basic α-amino
groups. In addition, each of the acidic and basic amino acids contains an
ionizable group in its side chain. Thus, both free amino acids and some amino
acids combined in peptide linkages can act as buffers. Recall that acids may be
defined as proton donors and bases as proton acceptors. Acids (or bases)
described as “weak” ionize to only a limited extent. The concentration of
protons in aqueous solution is expressed as pH, where pH = log 1/[H+]
or –log [H+]. The quantitative relationship between the pH of the
solution and concentration of a weak acid (HA) and its conjugate base (A-)
is described by the Henderson-Hasselbalch equation.
A. Derivation of the equation
Consider the release of
a proton by a weak acid represented by HA:

The “salt” or conjugate
base, A-, is the ionized form of a weak acid. By definition, the
dissociation constant of the acid, Ka, is
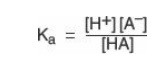
[Note: The larger the
Ka, the stronger the acid, because most of the HA has dissociated into H+
and A-. Conversely, the smaller the K a, the less acid has
dissociated and, therefore, the weaker the acid.] By solving for the [H+]
in the above equation, taking the logarithm of both sides of the equation,
multiplying both sides of the equation by –1, and substituting pH = –log [H+]
and pKa = –log Ka, we obtain the Henderson-Hasselbalch equation:

B. Buffers
A buffer is a solution
that resists change in pH following the addition of an acid or base. A buffer
can be created by mixing a weak acid (HA) with its conjugate base (A-).
If an acid such as HCl is added to a buffer, A- can neutralize it,
being converted to HA in the process. If a base is added, HA can neutralize it,
being converted to A- in the process. Maximum buffering capacity
occurs at a pH equal to the pKa, but a conjugate acid–base pair can still serve
as an effective buffer when the pH of a solution is within approximately ±1 pH
unit of the pKa. If the amounts of HA and A- are equal, the pH is
equal to the pKa. As shown in Figure 1.9, a solution containing acetic acid (HA
= CH3 – COOH) and acetate (A- = CH3 –COO–)
with a pKa of 4.8 resists a change in pH from pH 3.8 to 5.8, with maximum
buffering at pH 4.8. At pH values less than the pKa, the protonated acid form
(CH3 – COOH) is the predominant species in solution. At pH values
greater than the pKa, the deprotonated base form (CH3 – COO–) is the
predominant species.
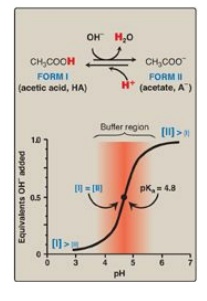
Figure 1.9 Titration curve of acetic acid.
C. Titration of an amino acid
1. Dissociation of the carboxyl group: The titration curve of an amino
acid can be analyzed in the same way as described for acetic acid. Consider
alanine, for example, which contains an ionizable α-carboxyl and α-amino group.
[Note: Its –CH3 R group is nonionizable.] At a low (acidic) pH, both
of these groups are protonated (shown in Figure 1.10). As the pH of the
solution is raised, the – COOH group of form I can dissociate by donating a
proton to the medium. The release of a proton results in the formation of the
carboxylate group, – COO–. This structure is shown as form II, which is the
dipolar form of the molecule (see Figure 1.10). This form, also called a
zwitterion, is the isoelectric form of alanine, that is, it has an overall
(net) charge of zero.
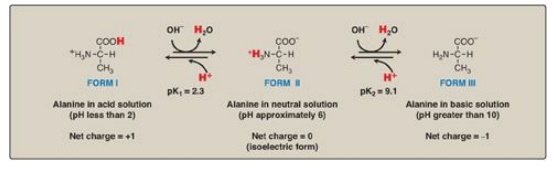
Figure 1.10 Ionic forms of alanine in acidic, neutral, and basic solutions.
2. Application of the Henderson-Hasselbalch
equation: The
dissociation constant of the carboxyl group of an amino acid is called K1,
rather than Ka, because the molecule contains a second titratable group. The
Henderson-Hasselbalch equation can be used to analyze the dissociation of the
carboxyl group of alanine in the same way as described for acetic acid:
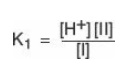
where I is the fully
protonated form of alanine, and II is the isoelectric form of alanine (see
Figure 1.10). This equation can be rearranged and converted to its logarithmic
form to yield:

3. Dissociation of the amino group: The second titratable group of
alanine is the amino (– NH3+) group shown in Figure 1.10.
This is a much weaker acid than the – COOH group and, therefore, has a much
smaller dissociation constant, K2. [Note: Its pKa is, therefore,
larger.] Release of a proton from the protonated amino group of form II results
in the fully deprotonated form of alanine, form III (see Figure 1.10).
4. pKs of alanine: The sequential dissociation of
protons from the carboxyl and amino groups of alanine is summarized in Figure
1.10. Each titratable group has a pKa that is numerically equal to the pH at
which exactly one half of the protons have been removed from that group. The
pKa for the most acidic group (–COOH) is pK1, whereas the pKa for
the next most acidic group (– NH3+) is pK2. [Note:
The pKa of the α-carboxyl group of amino acids is approximately 2, whereas that
of the α-amino is approximately 9.]
5. Titration curve of alanine: By applying the
Henderson-Hasselbalch equation to each dissociable acidic group, it is possible
to calculate the complete titration curve of a weak acid. Figure 1.11 shows the
change in pH that occurs during the addition of base to the fully protonated
form of alanine (I) to produce the completely deprotonated form (III). Note the
following:
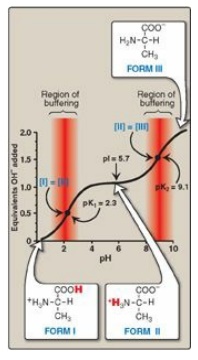
Figure 1.11 The titration curve of alanine.
a. Buffer pairs: The – ICOOH/–
ICOO– pair can serve as a buffer in
the pH region around pK1, and the – NH3+/– NH2
pair can buffer in the region around pK2.
b. When pH = pK: When the pH is equal to pK1 (2.3),
equal amounts of forms I and II of alanine exist in solution. When the pH is
equal to pK2 (9.1), equal amounts of forms II and III are present in
solution.
c. Isoelectric point: At neutral pH, alanine exists
predominantly as the dipolar form II in which the amino and carboxyl groups are
ionized, but the net charge is zero. The isoelectric point (pI) is the pH at
which an amino acid is electrically neutral, that is, in which the sum of the
positive charges equals the sum of the negative charges. For an amino acid,
such as alanine, that has only two dissociable hydrogens (one from the
α-carboxyl and one from the α-amino group), the pI is the average of pK1
and pK2 (pI = [2.3 + 9.1]/2 = 5.7) as shown i n Figure 1.11. The pI
is, thus, midway between pK1 (2.3) and pK2 (9.1). pI corresponds
to the pH at which the form II (with a net charge of zero) predominates and at
which there are also equal amounts of forms I (net charge of +1) and III (net
charge of –1).
Separation of plasma proteins by charge typically
is done at a pH above the pI of the major proteins. Thus, the charge on the
proteins is negative. In an electric field, the proteins will move toward the
positive electrode at a rate determined by their net negative charge.
Variations in the mobility pattern are suggestive of certain diseases.
6. Net charge of amino acids at neutral pH: At physiologic pH, amino acids
have a negatively charged group (– ICOO–)
and a positively charged group (– INH3+),
both attached to the α-carbon. [Note: Glutamate, aspartate, histidine,
arginine, and lysine have additional potentially charged groups in their side
chains.] Substances such as amino acids that can act either as an acid or a
base are defined as amphoteric and are referred to as ampholytes (amphoteric
electrolytes).
D. Other applications of the Henderson-Hasselbalch equation
The Henderson-Hasselbalch equation can be used to calculate how the pH of a physiologic solution responds to changes in the concentration of a weak acid and/or its corresponding “salt” form. For example, in the bicarbonate buffer system, the Henderson-Hasselbalch equation predicts how shifts in the bicarbonate ion concentration, [HCO3–], and CO2 influence pH (Figure 1.12A). The equation is also useful for calculating the abundance of ionic forms of acidic and basic drugs. For example, most drugs are either weak acids or weak bases (Figure 1.12B). Acidic drugs (HA) release a proton (H+), causing a charged anion (A-) to form.
HA ↔ H+
+ A-
Weak bases (BH+) can also release a H+. However, the protonated form of basic drugs is usually charged, and the loss of a proton produces the uncharged base (B).
BH+ ↔ B+H+
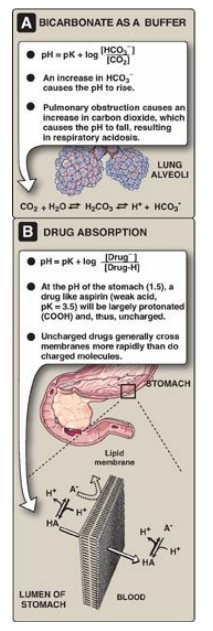
Figure 1.12 The Henderson-Hasselbalch equation is used to predict: A, changes in pH as the concentrations of HCO3– or CO2 are altered, or B, the ionic forms of drugs.
A drug passes through
membranes more readily if it is uncharged. Thus, for a weak acid, such as
aspirin, the uncharged HA can permeate through membranes, but A- cannot.
For a weak base, such as morphine, the uncharged form, B, penetrates through
the cell membrane, but BH+ does not. Therefore, the effective concentration of
the permeable form of each drug at its absorption site is determined by the
relative concentrations of the charged (impermeant) and uncharged (permeant)
forms. The ratio between the two forms is determined by the pH at the site of
absorption, and by the strength of the weak acid or base, which is represented
by the pKa of the ionizable group. The Henderson-Hasselbalch equation is useful
in determining how much drug is found on either side of a membrane that
separates two compartments that differ in pH, for example, the stomach (pH
1.0–1.5) and blood plasma (pH 7.4).
Related Topics
