Drug Concentration and Pharmacological Response
| Home | | Biopharmaceutics and Pharmacokinetics |Chapter: Biopharmaceutics and Pharmacokinetics : Drug Concentration and Pharmacological Response
The empirical approach in optimisation of drug therapy was based on relating pharmacological response to the dose administered.
Drug Concentration and Pharmacological Response
The empirical approach in optimisation of drug
therapy was based on relating pharmacological response to the dose
administered. There are several drawbacks of such an approach—tedious, time
consuming, costly, etc. Moreover, poor correlation may be observed between drug
dosage and response since a given dose or a dosing rate can result in large
deviations in plasma drug concentration which in most cases are attributable to
formulation factors and drug’s elimination characteristics. It is well
understood that the response correlates better with the plasma drug
concentration or with the amount of drug in the body rather than with the
administered dose. Thus, it is easy and more appropriate to design dosage
regimens by application of pharmacokinetic principles. The approach is based on
the principle that the response produced is proportional to the concentration
of drug at the site of action which in turn is reflected in the concentration
of drug in plasma. The mathematical
relationship between plasma drug concentration and pharmacological response are
called as pharmacokinetic-pharmacodynamic modelling (PK/PD modelling).
Problems in Developing PK/PD Relationship
The factors that complicate development of
concentration-response relationships are:
1. Delay in Drug Distribution: Most
sites of action are located in the extravascular tissues and equilibration with drug takes a long time. This
results in delay in observation of response. Long delays may occur when the
therapeutic response is an indirect measure of drug effect—for example, the
anticoagulant effect of dicoumarol is due to indirect inhibition and depletion
of clotting factors. Often, the therapeutic action in several such cases
outlasts the plasma drug concentration e.g. reserpine.
2. Protein Binding: Ideally, the pharmacological
response should be correlated with the
concentration of unbound drug in plasma since its activity is elicited only by
the free form. However, quantification of unbound drug is difficult and thus,
if the relationship is based on total plasma drug concentration, any variation
in the degree of binding will obscure it.
3. Active Metabolites: The
metabolites of some drugs such as imipramine and amitriptyline are active which obscure the concentration-response
relationship if it is based on the concentration of parent drug. Some drugs
such as propranolol form active metabolites on first-pass hepatic metabolism
and thus, result in greater response when administered orally than when given
intravenously.
4. Tolerance: The effectiveness of some drugs
decreases with chronic use due to development
of acquired tolerance. Tolerance may be pharmacokinetic i.e. through enhanced
metabolism e.g. carbamazepine or pharmacodynamic i.e. through diminished
response after some period of chronic use e.g. nitroglycerine.
5. Racemates: Several drugs are administered as
racemic mixture of two optically active
enantiomers of which usually one is active; for example, the S(+) isomer of
ibuprofen. Hence, a difference in the ratio of active to inactive isomer can
lead to large differences in pharmacological response.
Therapeutic Concentration Range
The therapeutic effectiveness of a drug depends
upon its plasma concentration. There is an optimum concentration range in which
therapeutic success is most likely and concentrations both above and below it
are more harmful than useful. This concentration range is called as therapeutic window or therapeutic range. Such a range is thus based on
the difference between pharmacological effectiveness and toxicity. The
wider it is the more is the ease in
establishing a safe and effective dosage regimen. The therapeutic ranges of
several drugs have been developed. For many, the range is narrow and for
others, it is wide (see Table 13.1).
TABLE 13.1
Therapeutic Range for Some Drugs
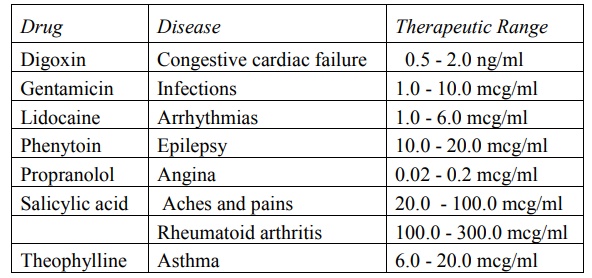
Some drugs can be used to treat several diseases
and will have different ranges for different conditions e.g. salicylic acid is
useful both in common aches and pains as well as in rheumatoid arthritis. The
upper limit of the therapeutic range may express loss of effectiveness with no
toxicity e.g. tricyclic antidepressants or reflect toxicity which may be
related to pharmacological effect of the drug e.g. hemorrhagic tendency with
warfarin or may be totally unrelated e.g. ototoxicity with aminoglycosides.
Concentration-Response Relationships – Pharmacodynamic Models
With most drugs, the response produced is
reversible i.e. a reduction in concentration at the site of action reverses the
effect. The response produced by a drug can be classified into two categories –
1. Graded response - is the one where intensity of
effect increases with the dose or concentration
of drug. A majority of drugs produce graded response. The response can be measured on a continual
basis in such cases and establishing a linear relationship between drug
concentration and intensity of response is easy.
2. Quantal Response – is the one where the drugs may either show their effect or not at all i.e. the responses are not observed on a continuous basis, for example, prevention of seizures by phenytoin.
Such responses are also called as all-or-none responses. Thus,
establishing a concentration-response relationship in such circumstances is
difficult but can be developed in terms of the frequency with which a particular event occurs at a given drug
concentration.
Mathematical models that relate pharmacological effect to a measured
drug concentration in plasma or at the effector site can be used to develop
quantitative relationships. Such models are often called as pharmacodynamic models. Some of the commonly used
relationships or models are discussed below.
1. Linear Model: When the pharmacological effect
(E) is directly proportional to the drug
concentration (C), the relationship may be written as:
E = PC + E0 (13.1)
where P is the slope of the line obtained from a
plot of E versus C and Eo is the extrapolated y-intercept called as baseline effect in the absence of drug.
2. Non-linear/Logarithmic Model: If the
concentration-effect relationship does not
conform to a simple linear function, a logarithmic transformation of the
data is needed.
E = PlogC + 1 (13.2)
where I
is empirical constant. This transformation is popular because it expands the
initial part of the curve where response is changing markedly with a small
change in concentration and contracts the latter part where a large change in
concentration produces only a slight change in response. An important feature
of this transformation is the linear relationships between drug concentration
and response at concentrations producing effects of between 20 to 80% of the
maximum effect (Fig. 13.1). Beyond this range, a larger dose produces a larger
concentration of drug in the body.
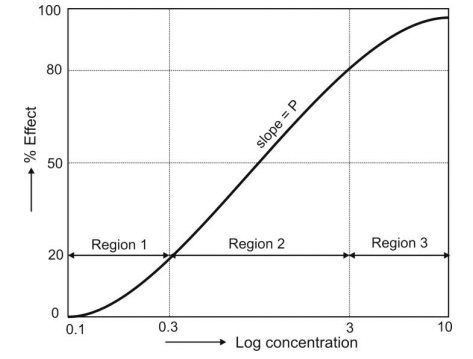
Fig. 13.1 A typical sigmoidal shape log drug concentration-effect relationship
3. Emax Model/Hyperbolic Model: Unlike earlier models, these models describe non-linear concentration-effect relationships i.e. the response
increases with an increase in drug concentration at low concentrations and
tends to approach
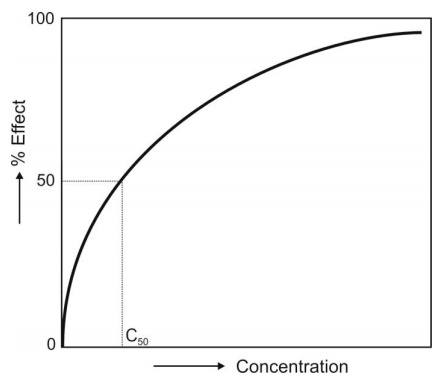
Fig. 13.2 A hyperbolic concentration-response relationship based on Emax model
maximum (asymptote) at high concentrations (Fig.
13.2). Such a plot is characteristic of most concentration-response curves.
None of the preceding models can account for the maximal drug effect as the Emax models.
Michaelis-Menten equation for a
saturable process (saturation of receptor sites by the drug molecules) is used to describe such a model.
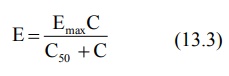
where
Emax = maximum effect, and
C50 = the
concentration at which 50% of the effect is produced.
When C << C50, the equation
reduces to a linear relationship. In the range 20 to 80%, the Emax
model approximates equation 13.2.
4. Hill Model/Sigmoid-Emax Model: In certain cases, the concentration-response relationship is steeper or shallower than that predicted from
equation 13.3. A better fit may otherwise be obtained by considering the shape factor ‘h’, also called as Hill coefficient,
to account for deviations from a perfect hyperbola, and the equation so obtained is called Hill equation (equation
13.4).
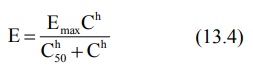
If h = 1, a normal hyperbolic plot is obtained and
the model is called Emax model. Larger the value of h, steeper the
linear portion of the curve and greater its slope. Such a plot is often
sigmoidal and thus, the Hill model may also be called as sigmoid-Emax model
(Fig. 13.3).
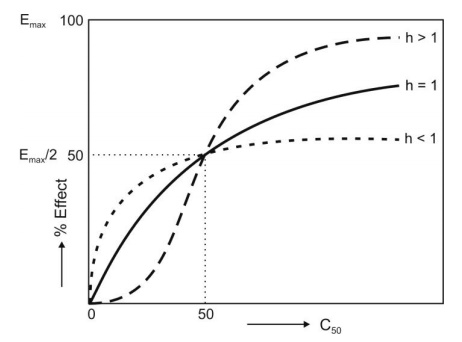
Fig. 13.3 Effect of shape factor n on the
concentration-response curves
Onset/Duration of Effect-Concentration Relationships
The onset of action of a drug that produces quantal
response occurs when a minimum effective level of drug in the plasma Cmin
is reached. The duration of action of such a drug will depend upon how long the
plasma concentration remains above the Cmin level.
The factors which influence duration of action of a
drug are:
1. The dose size, and
2. The rate of drug removal from
the site of action which in turn depends upon the redistribution of drug to
poorly perfused tissues and elimination processes.
An increase in dose promotes rapid onset of action
by reducing the time required to reach the Cmin and prolongs the
duration of effect. The influence of dose on duration of action can be explained
as follows. Consider a drug that distributes rapidly (one-compartment kinetics)
and administered as i.v. bolus dose. The plasma drug concentration is given by
the equation:
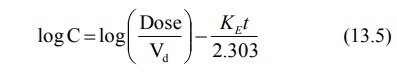
The plasma concentration falls eventually to a level
Cmin below which the drug does not show any response. At this time,
t = td, the duration of effect of a drug. The above equation thus
becomes:
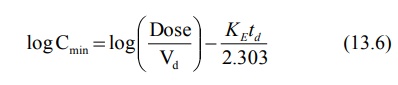
Rearranging to define duration of effect, the
equation is:
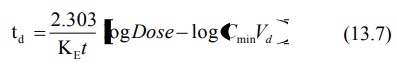
where CminVd = Xmin, the minimum amount of drug in the body required to produce a response. A plot of td versus log dose yields a straight line with slope 2.303/KE and x-intercept at zero duration of effect of log Xmin (Fig. 13.4).
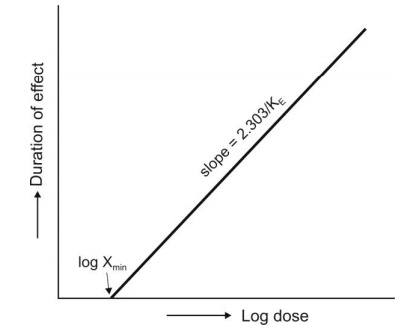
Fig. 13.4 Relationship between dose of drug and duration of action
Equation 13.7 shows that the duration of effect is
also a function of t½ (0.693/KE). With each doubling of
dose the duration of effect increases by one half-life. This can be explained
by considering that a dose Xo produces a duration of effect td;
so when double the dose i.e. 2Xo is administered, the dose remaining
after one half-life will be Xo which can produce a duration of
effect equal to td. Thus, the total duration of effect produced by
2Xo will be t½ + td. However, the approach of
extending the duration of action by increasing the dose is harmful if the drug
has a narrow therapeutic index. An alternative approach is to administer the
same dose when the drug level has fallen to Xmin. Thus, after the
second dose, the drug in the body will be (dose + Xmin). If Xmin
is small in relation to dose, very little increase in duration of action will
be observed.
Intensity of Effect-Concentration Relationships
In case of a drug that produces quantal response, the pharmacodynamic parameter that
correlates better with its concentration is duration of action. The
parameter intensity of
response is more useful for
correlation with the concentration of a drug that shows graded effect. Like duration of action, intensity of action also
depends upon the dose and rate of
removal of drug from the site of action. The intensity of action also depends
upon the region of the concentration-response curve (refer Fig. 13.1). If a drug with rapid distribution characteristics
is given as i.v. bolus dose large enough to elicit a maximum response, the log
concentration-response plot obtained will be as shown in Fig. 13.1. The
relationship between dose, intensity of effect and time can be established by
considering the plots depicted in Fig. 13.5. which also shows 3 regions.
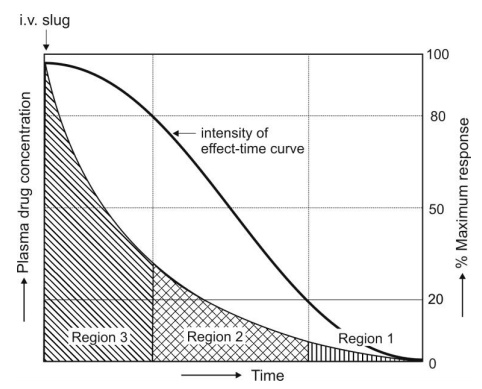
Fig. 13.5 The fall in intensity of response with drug concentration and with time following administration of a single
i.v. bolus dose.
Region 3 indicates 80 to 100% maximum response. The
initial concentration of drug after
i.v. bolus dose lies in this region if the dose injected is sufficient to
elicit maximal response. The drug concentration falls rapidly in this region
but intensity of response remains maximal and almost constant with time.
Region 2 denotes 20 to 80% maximum response. In this
region, the intensity of response is
proportional to log of drug concentration and expressed by equation 13.2.
Intensity of Effect = P log C + I (13.2)
Since the decline in drug concentration is a
first-order process, log C can be expressed as:
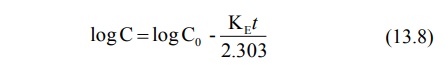
Substituting 13.8 in equation 13.2. and rearranging
we get:
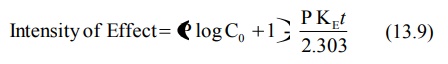
If Eo is the intensity of response when
concentration is Co, then:
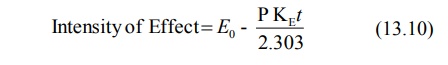
Equation 13.10 shows that the intensity of response
falls linearly (at a constant zero-order rate) with time in region 2. This is
true for most of the drugs. The drug concentration however declines
logarithmically or exponentially in region 2 as shown by equation 13.8.
Region 1 denotes 0 to 20% maximum response. In this
region, the intensity of effect is
directly proportional to the drug concentration but falls exponentially with
time and parallels the fall in drug concentration.
Related Topics
