Pharmacokinetic Principles in the Design and Fabrication of Controlled-Release Drug Delivery Systems
| Home | | Biopharmaceutics and Pharmacokinetics |Chapter: Biopharmaceutics and Pharmacokinetics : Controlled Release Medication
The controlled-release dosage forms are so designed that they release the medicament over a prolonged period of time usually longer than the typical dosing interval for a conventional formulation.
PHARMACOKINETIC PRINCIPLES IN THE DESIGN AND FABRICATION OF
CONTROLLED-RELEASE DRUG DELIVERY SYSTEMS
The controlled-release dosage forms are so designed
that they release the medicament over a prolonged period of time usually longer
than the typical dosing interval for a conventional formulation. The drug
release rate should be so monitored that a steady plasma concentration is
attained by reducing the ratio Css,max/C ss,min while
maintaining the drug levels within the therapeutic window. The rate-controlling
step in the drug input should be determined not by the absorption rate but by
the rate of release from the formulation which ideally should be slower than
the rate of absorption. In most cases, the release rate is so slow that if the
drug exhibits two-compartment kinetics with delayed distribution under normal
circumstances, it will be slower than the rate of distribution and one can,
thus, collapse the plasma
concentration-time profile in such instances into a one-compartment model i.e. a one-compartment model is suitable and applicable for the design of
controlled-release drug delivery systems. Assuming that the KADME of a drug are first-order
processes, to achieve a steady, non-fluctuating plasma concentration, the rate
of release and hence rate of input of drug from the controlled-release dosage
form should be identical to that from constant rate intravenous infusion. In
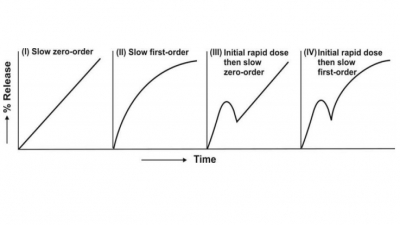
other words, the rate of drug release from such a system should ideally be
zero-order or near zero-order. One can thus treat the desired release rate Ro
of controlled drug delivery system according to constant rate i.v. infusion. In
order to maintain the desired steady-state concentration Css, the
rate of drug input, which is zero-order release rate (Ro), must be
equal to the rate of output (assumed to be first-order elimination process).
Thus:
R0 = Routput (14.1)
The rate of drug output is given as the product of
maintenance dose DM and first-order elimination rate constant KE.
Routput = DMKE (14.2)
For a zero-order constant rate infusion, the rate
of output is also given as:
Routput = KE Css Vd
(14.3)
Since ClT = KE Vd,
the above equation can also be written as:
Routput = CssClT (14.4a)
Or R0 = Css ClT (14.4b)
The bioavailability of a drug from controlled-release
dosage form cannot be 100% as the total release may not be 100% and the drug
may also undergo presystemic metabolism. Hence, if F is the fraction
bioavailable, then:
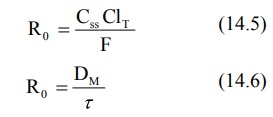
Substituting equation 14.6 in equation 14.5 and rearranging, we get:
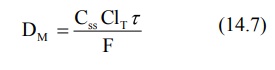
where τ = dosing interval.
From the above equation, one can calculate the dose
of drug that must be released in a given period of time in order to achieve the
desired target steady-state concentration. It also shows that total systemic
clearance is an important parameter in such a computation.
Since attainment of steady-state levels with a
zero-order controlled drug release system would require a time period of about
5 biological half-lives, an immediate-release dose, DI, called as loading
dose, may be incorporated in such a system in addition to the
controlled-release components. The total dose, DT needed to maintain
therapeutic concentration in the body would
then be:
DT = DI + DM (14.8)
The immediate-release dose is meant to provide the
desired steady-state rapidly and can be calculated by equation:
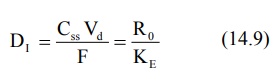
The above equation ignores the possible additive
effect from the immediate and controlled-release components. For many
controlled-release products, there is no built-in loading dose.
The dosing interval for a drug following
one-compartment kinetics with linear disposition is related to elimination
half-life and therapeutic index TI according to equation:
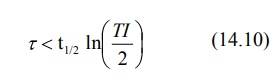
Related Topics