Fundamental Aspects of Crushing and Grinding

FUNDAMENTAL ASPECTS OF CRUSHING AND GRINDING

A basic study of crushing and grinding considers the physical properties of the material, the crushing mechanism itself, and its relation to the mechanism of failure. When a stress, which may be compressive, tensile, or shear, is applied to a solid, the latter deforms. Initially, the deformation or strain is the distortion of the crystal lattice by relative displacement of its components without change of structure. Complete recovery follows the removal of the stress, and behavior is elastic. Figure 12.1 considers the deformation of a solid under a tensile stress, and elastic behavior is shown over section AB. Below the elastic limit, B, stress is proportional to strain and is related to it by various moduli. Beyond the yield point, C, permanent or plastic deformation occurs and, as shown by release of stress at point D, all strain is not recoverable. Sliding along natural cleavage planes is occurring in this region. Plastic deformation is terminated by failure or fracture, which is normally a quite gradual and reproducible process preceded by thinning of the material. The stress at point E is a measure of the strength of the material. The area under the curve at any point represents the strain energy per unit volume absorbed by the specimen up to that strain. The limiting strain energy per unit volume is the energy absorbed up to the point of failure.

An extensive period of plastic deformation is shown in Figure 12.1, and the material would be classified as ductile. For the brittle materials normally encountered in grinding, little plastic deformation takes place and the points C and E almost coincide. 

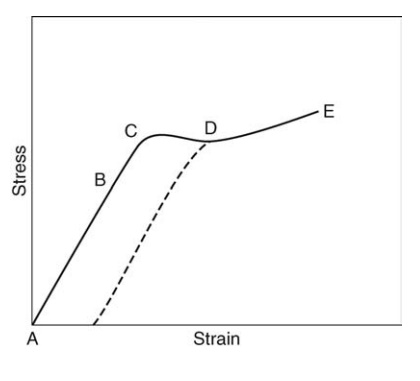
FIGURE 12.1 The tensile deformation of a ductile material

Fracture is explained here in terms of cracks and flaws naturally present in the material. It occurs suddenly and with shattering. The energy employed in stressing the particle to the point of failure reappears mainly as heat on release of strain in a manner analogous to the sudden release of a stressed spring.

The theoretical strength of crystalline materials can be calculated from interatomic attractive and repulsive forces. The strength of real materials is, however, found to be many times smaller than the theoretical value. The dis-crepancy is explained in terms of flaws of various kinds, such as minute fissures or irregularities of lattice structure known as dislocations. These have the capacity to concentrate the stress in the vicinity of the flaw. Failure may then occur at a much lower overall stress than is predicted from the theoretical considerations. Failure occurs with the development of a crack tip, which propagates rapidly through the material, penetrating other flaws, which may, in turn, produce secondary cracks. The strength of the material therefore depends on the random distribution of flaws and is a statistical quantity varying within fairly wide limits. This concept explains why a material becomes progressively more difficult to grind. Since the probability of containing an effective flaw decreases as the particle size decreases, the strength will increase until, with the achievement of faultless domains, the strength of the material will equal the theoretical strength. This position is not realized in practice because of com-plicating factors such as aggregation.

The strength of most materials is greater in compression than in tension. It is therefore unfortunate that technical difficulties prevent the direct use of ten-sile stresses. The compressive stresses commonly used in comminution equip-ment do not cause failure directly but generate, by distortion, sufficient tensile or shear stress to form a crack tip in a region away from the point of primary stress application. This is an inefficient but unavoidable mechanism. Impact and attrition are the other basic modes of stress application. The distinction between impact and compression is referred to below. Attrition, which is commonly employed, is difficult to classify but is probably, primarily, a shear mechanism.

In any machine, one mode of stress application usually predominates. It must be correctly chosen with respect to the mechanical properties of the material. Compression, for example, is useless for comminution of fibrous or waxy solids. Attrition is generally necessary for all fine grinding.

The deformation and subsequent failure of a brittle material is a function not only of stress but also of the rate at which the stress is applied. Different results may be obtained from slow compressive breaking and impact breaking at the same energy. Particle shape, size, and size distribution may be affected. In impact breaking, the rate of stress application is so high that the limiting strain energy may be exceeded several times by the suddenness of the operation. This is because fracture is time dependent, a lag occurring between the application of maximum stress and failure.

Stress application is further complicated by “free-crushing” and “packed-crushing” mechanisms. In free crushing, the stress is applied to an uncon-strained particle and released when failure occurs. In packed crushing, the application of stress continues on the crushed bed of particles. Although further size reduction occurs, the process is less efficient because of vitiation of energy by the effects of interparticulate friction and stress transmission via particles that do not themselves fracture. This is easily demonstrated when a crystalline material is ground in a pestle and mortar. The fine powder initially produced protects coarser particles. If the material is sieved and oversize particles are returned, the operation may be completed with far less effort.

Free crushing is most nearly approached in the roller mill, which explains the high efficiency of the machine, and, to a lesser extent, in other continuous processes in which individual particles are presented to the grinding media. Packed crushing occurs in ball mills.