The Efficiency of Grinding

THE EFFICIENCY OF GRINDING

Extensive investigation of the relation between the energy supplied to a mill and the size reduction achieved has been carried out. The efficiency of the process reflected by such a relation is of small importance in pharmacy because the applications are limited. For completeness, however, they are considered below.

Most of the energy supplied to the mill is ultimately dissipated as heat because of mechanical inefficiency. Most of the remainder or net grinding energy also appears as heat produced upon the release of strain energy, a small part being added to the internal energy of the system as, for example, surface energy.

Various hypotheses relate the net grinding energy applied to a process and the size reduction achieved. The first, proposed by Karl von Rittinger in 1867, states that the energy necessary for size reduction is directly proportional to the increase in surface area.

E = k(S_p - S_f)                            (12:1)

where E is the energy consumed, and S_p and S_f are the surface areas of product and feed materials, respectively. The constant, k, depends on the grinding unit employed and represents the energy consumed in enlarging the surface area by one unit. The relation between surface area and particle size has already been derived, and we may therefore write

where d_f and d_p are the particle sizes of feed and product particles, respectively. The hypothesis indicates that energy consumption per unit area of new surface produced increases faster than the linear ratio of feed and product dimensions, a phenomenon already noted and explained. The proportionality of net energy input and new surface produced has been confirmed in some grinding operations.

Although Rittinger’s law is concerned with surfaces and not the energy associated with those surfaces, it is rational to relate crushing energy con-sumed and the surface energy gained by increase of surface area, thereby arriving at a measure of efficiency. In experiments in which single particles are crushed, between 1% and 30% of the applied energy appears as surface energy. In practical systems, when application of stress is less ideal, the net grinding energy is 100 to 1000 times greater than that associated with the new surface, that is, the efficiency of the process, on this basis, is between 0.1% and 1%.

The relation of energy to surface area provides little information on the grinding process and does not influence mill design. It, however, provides the basis of some grindability tests in which a known amount of energy is supplied to a mill and the increase in surface is measured. This application is restricted to fine grinding.

Conversion of grinding energy to surface energy is neglected in Kick’s law, enunciated in 1885. The law is based on the deformation and brittle failure of elastic bodies and states that the energy required to produce analogous changes of configuration of geometrically similar bodies is proportional to the weight or volume of those bodies. The energy requirements are independent of the initial particle size and depend only on the size reduction ratio. Kick’s law predicts lower energies than the relation proposed by Rittinger. The theory, however, demands that the resistance to crushing does not change with particle size. The role of flaws present in real materials is not considered with the result that the energy required for fine grinding, when the apparent strength may have greatly risen, is underestimated.

A third theory of comminution gives results intermediate between the predictions of the laws of Kick and Rittinger (Bond, 1952). The theory rests on three principles, the first of which states that any divided material must have a positive energy register. This can only be zero when the particle size becomes infinite. The input energy, E, for any size reduction process then equals the product energy register minus the feed energy register. The energy associated with a powder increases as the particle size decreases, and we may assume that the energy register is inversely proportional to the particle size to an exponent, n. Hence,

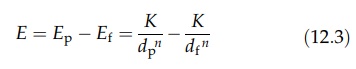
The second principle of Bond’s theory assigns to n a value of i, stating that “total work useful in breaking which has been applied to a stated weight of an homogeneous material is inversely proportional to the square root of the diameter of the product particles.”

The third principle states that breakage of the material is determined by the flaw structure. This aspect of size reduction has already been discussed.

A modification to Kick’s law, sometimes known as the fourth law of comminution, has also been proposed. For its discussion, the reader is referred to the original paper (Holmes, 1957)

An empirical but realistic approach to mill efficiency is gained through experiments in which the energy consumed and size reduction achieved are compared with values obtained in a laboratory test operating under free-crushing conditions. All energy supplied in the latter is available for crushing, and the test is assumed to be 100% efficient. Both slow crushing and impact tests are used. A large number of single particles may be simultaneously crushed, and the work done may be measured (Carey and Stairand, 1953). The latter is then related to the size reduction achieved. Similar measurements can be made during practical milling, expressing the efficiency of the process as a percentage of the free-crushing value. On this basis, approximate efficiency of the roll crusher is 80%, that of the swing hammer mill is 40%, that of the ball mill is 10%, and that of the fluid energy mill is only 1%.