Sensitivity to Outliers, Outlier Rejection, and Robust Regression
| Home | | Advanced Mathematics |Chapter: Biostatistics for the Health Sciences: Correlation, Linear Regression, and Logistic Regression
Outliers refer to unusual or extreme values within a data set. We might expect many biochemical parameters and human characteristics to be normally distributed, with the majority of cases falling between ±2 standard deviations.
SENSITIVITY TO OUTLIERS, OUTLIER REJECTION, AND ROBUST REGRESSION
Outliers refer to unusual or extreme values within
a data set. We might expect many biochemical parameters and human
characteristics to be normally distributed, with the majority of cases falling
between ±2 standard deviations. Nevertheless, in a large data set, it is
possible for extreme values to occur. These extreme values may be caused by actual
rare events or by measurement, coding, or data entry errors. We can visualize
outliers in a scatter diagram, as shown in Figure 12.4.
The least squares method of regression calculates “b” (the regression slope) and “a”
(the intercept) by minimizing the sum of squares [Σ(Y – Yˆ)2] about the regres
Figure 12.4. Scatter diagram with outliers.
Even a few outliers may impact both the intercept
and the slope of a regression line. This strong impact of outliers comes about
because the penalty for a deviation from the line of best fit is the square of
the residual. Consequently, the slope and in-tercept need to be placed so as to
give smaller deviations to these outliers than to many of the more “normal”
observations.
The influence of outliers also depends on their
location in the space defined by the distribution of measurements for X (the independent variable).
Observations for very low or very high values of X are called leverage points and have large effects on the slope of
the line (even when they are not outliers). An alternative to least squares
regression is robust regression, which is less sensitive to outliers than is
the least squares model. An example of robust regression is median regression,
a type of quantile regression, which is also called a minimum absolute
deviation model.
A very dramatic example of a major outlier was the
count of votes for Patrick Buchanan in Florida’s Palm Beach County in the now
famous 2000 presidential election. Many people believe that Buchanan garnered a
large share of the votes that were intended for Gore. This result could have
happened because of the confus-ing nature of the so-called butterfly ballot.
In any case, an inspection of two scatter plots
(one for vote totals by county for Buchanan versus Bush, Figure 12.5, and one
for vote totals by county for Buchanan versus Gore, Figure 12.6) reveals a
consistent pattern that enables one to predict the number of votes for Buchanan
based on the number of votes for Bush or Gore. This prediction model would work
well in every county except Palm Beach, where the votes for Buchanan greatly
exceeded expectations. Palm Beach was a very obvious outlier. Let us look at
the available data published over the Internet.
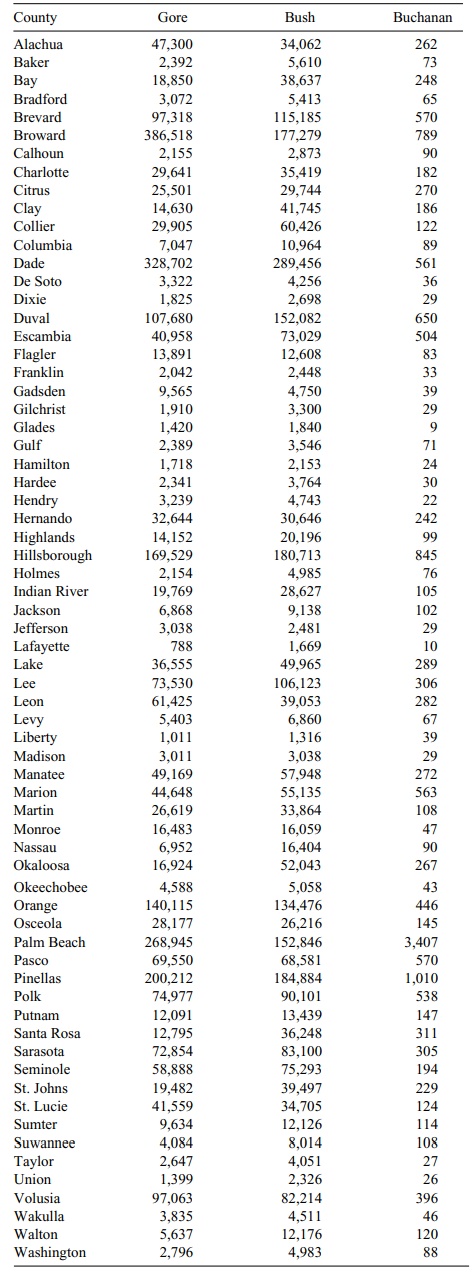
Table 12.6 shows the counties and the number of
votes that Bush, Gore, and Buchanan received in each county. The number of
votes varied largely by the size of the county; however, from a scatter plot
you can see a reasonable linear relation
TABLE 12.6. 2000 Presidential Vote by County in Florida
One could form a regression
equation to predict the total number of votes for Buchanan given that the total
number of votes for Bush is known. Palm Beach County stands out as a major
exception to the pattern. In this case, we have an outlier that is very
informative about the problem of the butterfly ballots.
Palm Beach County had by far the largest number of
votes for Buchanan (3407 votes). The county that had the next largest number of
votes was Pinellas County, with only 1010 votes for Buchanan. Although Palm
Beach is a large county, Broward and Dade are larger; yet, Buchanan gained only
789 and 561 votes, re-spectively, in the latter two counties.
Figure 12.5 shows a scatterplot of the votes for
Bush versus the votes for Buchanan. From this figure, it is apparent that Palm
Beach County is an outlier.
Next, in Figure 12.6 we see the same pattern we saw
in Figure 12.5 when com-paring votes for Gore to votes for Buchanan, and in
Figure 12.7, votes for Nader to votes for Buchanan. In each scatter plot, the
number of votes for any candidate is proportional to the size of each county,
with the exception of Palm Beach County. We will see that the votes for Nader
correlate a little better with the votes for Buchanan than do the votes for
Bush or for Gore; and the votes for Bush correlate somewhat better with the
votes for Buchanan than do the votes for Gore. If we ex-clude Palm Beach County
from the scatter plot and fit a regression function with or
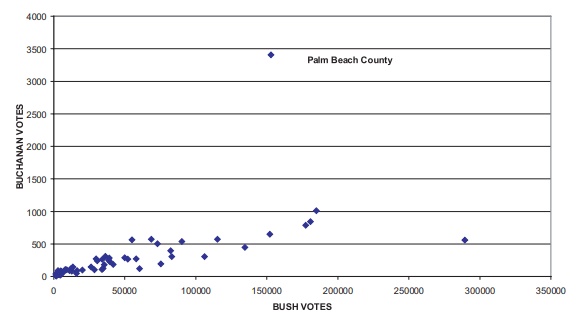
Figure 12.5. Florida presidential vote (all counties).
For example, Figures 12.8 and Figures 12.9 show the
regression equations with and without intercepts, respectively, for predicting
votes for Buchanan as a function of votes for Nader based on all counties
except Palm Beach. We then use these equations to predict the Palm Beach
outcome; then we compare our results to the
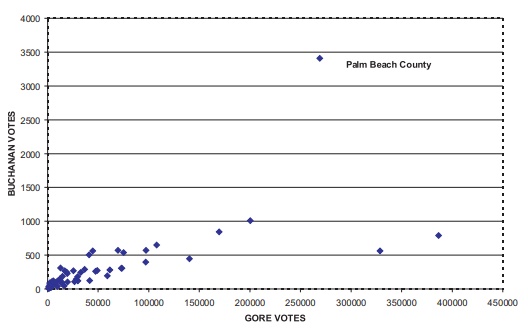
Figure 12.6. Florida presidential votes (all
counties).
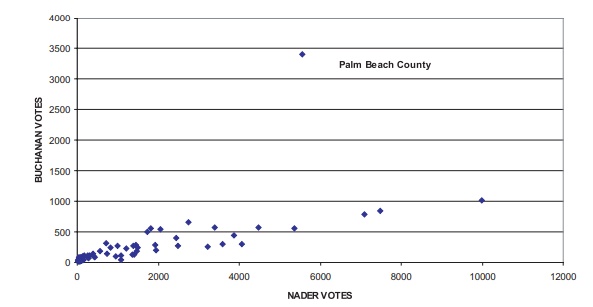
Figure 12.7. Florida presidential votes (all counties).
Since Nader received 5564 votes in Palm Beach County, we derive, using the equation in Figure 12.8, the prediction of Y for Buchanan: Yˆ = 0.1028(5564) + 68.93 = 640.9092. Or, if we use the zero intercept formula, we have Yˆ = 0.1194 (5564) = 664.3416.
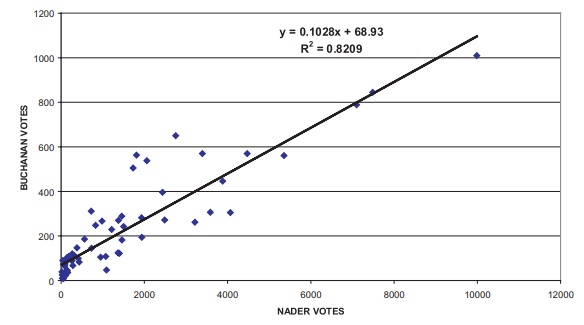
Figure 12.8. Florida presidential vote (Palm
Beach county omitted).
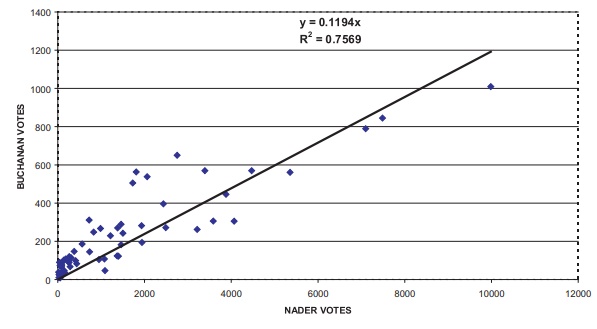
Figure 12.9. Florida presidential vote (Palm Beach county omitted).
Similar predictions for the votes for Buchanan using the votes for Bush as the covariate X
give the equations Yˆ = 0.0035 X + 65.51 = 600.471 and Yˆ = 0.004 X = 611.384 (zero intercept formula), since Bush reaped 152,846
votes in Palm Beach County. Votes for Gore also could be used to predict the
votes for Buchanan, although the correlation is lower (r = 0.7940 for the equation with intercept, and r = 0.6704 for the equation without the
intercept).
Using the votes for Gore, the regression equations
are Yˆ = 0.0025 X + 109.24 and Yˆ =
0.0032 X, respectively, for the fit
with and without the intercept. Gore’s 268,945 votes in Palm Beach County lead to predictions of 781.6025 and
1075.78 using the intercept and nonintercept equations, respectively.
In all cases, the predictions of votes for Buchanan
ranged from around 600 votes to approximately 1076 votes—far less than the 3407
votes that Buchanan actually received. This discrepancy between the number of
predicted and actual votes leads to a very plausible argument that at least
2000 of the votes awarded to Buchanan could have been intended for Gore.
An increase in the number of votes for Gore would
eliminate the outlier with re-spect to the number of votes cast for Buchanan
that were detected for Palm Beach County. This hypothetical increase would be
responsive to the complaints of many voters who said they were confused by the
butterfly ballot. A study of the ballot shows that the punch hole for Buchanan
could be confused with Gore’s but not with that of any other candidate. A
better prediction of the vote for Buchanan could be obtained by multiple
regression. We will review the data again in Section 12.9.
The undo influence of outliers on regression
equations is one of the problems that can be resolved by using robust
regression techniques. Many texts on regres-sion models are available that
cover robust regression and/or the regression diag-nostics that can be used to
determine when the assumptions for least squares regres-sion do not apply. We
will not go into the details of these topics; however, in Section 12.12 (Additional
Reading), we provide the interested reader with several good texts. These texts
include Chatterjee and Hadi (1988); Chatterjee, Price, and Hadi (1999); Ryan
(1997); Montgomery, and Peck (1992); Myers (1990); Draper, and Smith (1998);
Cook (1998); Belsley, Kuh, and Welsch (1980); Rousseeuw and Leroy (1987);
Bloomfield and Steiger (1983); Staudte and Sheather (1990); Cook and Weisberg
(1982); and Weisberg (1985).
Some of the aforementioned texts cover diagnostic
statistics that are useful for detecting multicollinearity (a problem that
occurs when two or more predictor vari-ables in the regression equation have a
strong linear interrelationship). Of course, multicollinearity is not a problem
when one deals only with a single predictor. When relationships among
independent and dependent variables seem to be nonlin-ear, transformation
methods sometimes are employed. For these methods, the least squares regression
model is fitted to the data after the transformation [see Atkinson (1985) or
Carroll and Ruppert (1988)].
As is true of regression equations, outliers can
adversely affect estimates of the correlation coefficient. Nonparametric
alternatives to the Pearson product moment correlation exist and can be used in
such instances. One such alternative, called Spearman’s rho, is covered in
Section 14.7.
Related Topics
