Testing Hypotheses about the Correlation Coefficient
| Home | | Advanced Mathematics |Chapter: Biostatistics for the Health Sciences: Correlation, Linear Regression, and Logistic Regression
In addition to assessing the strength of association between two variables, we need to know whether their association is statistically significant.
TESTING HYPOTHESES ABOUT THE CORRELATION COEFFICIENT
In addition to assessing the strength of
association between two variables, we need to know whether their association is
statistically significant. The test for the significance of a correlation
coefficient is based on a t test. In
Section 12.4, we presented r (the
sample statistic for correlation) and ρ (the population parameter for the correlation between X and Y in the population).
The test for the significance of a correlation
evaluates the null hypothesis (H0)
that ρ = 0 in
the population. We assume Y = α + bx + ε. Testing ρ = 0 is the same as testing b
= 0. The term ε in the equation is called the noise term or error term. It is also
sometimes referred to as the residual term. The assumption required for hypothesis
testing is that the noise term has a normal distribution with a mean of zero
and unknown variance σ2 independent of X. The significance test for Pearson’s correlation coefficient is
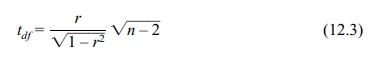
where df = n
– 2; n = number of pairs.
Referring to the earlier example presented in Table
12.2, we may test whether the previously obtained correlation is significant by
using the following procedure:
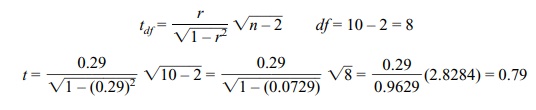
where p = n.s., t critical = 2.306, 2-tailed.
Related Topics
