Pearson’s Product Moment Correlation Coefficient and Its Sample Estimate
| Home | | Advanced Mathematics |Chapter: Biostatistics for the Health Sciences: Correlation, Linear Regression, and Logistic Regression
The formulae for a Pearson sample product moment correlation coefficient (also called a Pearson correlation coefficient).
PEARSON’S PRODUCT MOMENT CORRELATION COEFFICIENT AND ITS SAMPLE ESTIMATE
The formulae for a Pearson sample product moment
correlation coefficient (also called a Pearson correlation coefficient) are
shown in Equations 12.1 and 12.2. The deviation score formula for r is

We will apply these formulae to the small sample of
weight and height measure-ments shown in Table 12.2. The first calculation uses
the deviation score formula (i.e., the difference between each observation for
a variable and the mean of the variable).
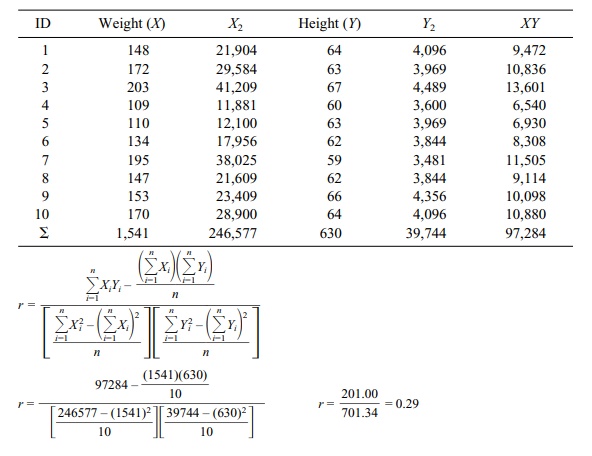
The data needed for the formulae are shown in Table
12.3. When using the cal-culation formula, we do not need to create difference
scores, making the calcula-tions a bit easier to perform with a hand-held
calculator.
We would like to emphasize that the Pearson product
moment correlation mea-sures the strength of the linear relationship between
the variables X and Y. Two variables X and Y can have an exact
non-linear functional relationship, implying a form of dependence, and yet have
zero correlation. An example would be the func-tion y = x2 for x between –1 and +1. Suppose that X is uniformly distributed on [0, 1] and
Y = X2 without any error term. For a bivariate distribution,
r is an estimate of the correlation (ρ) between X and Y, where
ρ = Cov(X, Y) / √[Var(X)Var(Y)]
The covariance between X and Y defined by Cov(X, Y)
is E[(X – μx)(Y – μy)], where μx and μy are, respectively, the population means for X and Y. We will show that Cov(X, Y)
= 0 and, consequently, ρ = 0. For those who know calculus, this proof is
TABLE 12.2. Deviation Score Method for Calculating r (Pearson Correlation Coefficient)
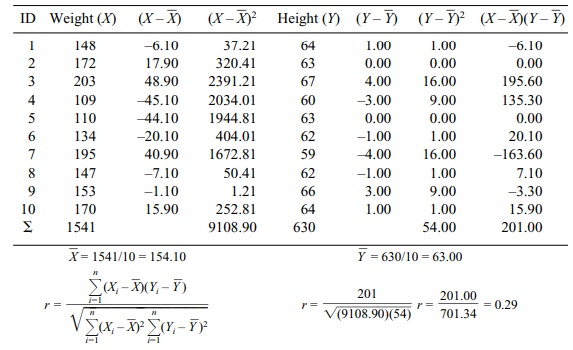
TABLE 12.3. Calculation Formula Method for Calculating r (Pearson Correlation Coefficient)
Display 12.1: Proof of Cov(X, Y) = 0 and ρ = 0 for Y = X 2

Related Topics
