Simpson’s Paradox in the 2 × 2 Table
| Home | | Advanced Mathematics |Chapter: Biostatistics for the Health Sciences: Categorical Data and Chi-Square Tests
Sometimes, as in a meta-analysis, it may be reasonable to combine results from two or more experiments that produce 2 × 2 contingency tables.
SIMPSON’S PARADOX IN THE 2 × 2 TABLE
Sometimes, as in a meta-analysis, it may be
reasonable to combine results from two or more experiments that produce 2 × 2
contingency tables. We simply cumulate the totals in the individual contingency
tables into the corresponding cells for the combined table. An apparent paradox
called Simpson’s paradox can result, howev-er. In Simpson’s paradox, we see a
particular association in each table but when we combine the tables the
association disappears or is reversed!
To see how this can happen, we take the following
fictitious example from Lloyd (1999, pages 153–154). In this example, a new
cancer treatment is applied to patients in a particular hospital and the
patients are classified as terminal and non-terminal. Before considering the
groups separately we naively think that we can evaluate the effectiveness of
the treatment by simply comparing its effect on both terminal and nonterminal
patients combined. The hospital has records that can be used to compare
survival rates over a fixed period of time (say 2 years) for patients on the
new treatment and patients taking the standard therapy. The hospital records
the results in 2 × 2 tables to see if the new treatment is more effective for
each of the groups. This results in the following 2 × 2 tables taken from Lloyd
(1999) with permission.
Table for All Patients
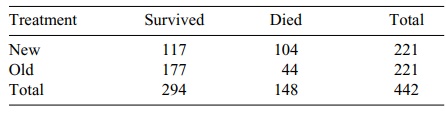
By examining the table, the result seems clear. In
each treatment group, 221 pa-tients got the treatment but 60 more patients
survived in the old treatment compared to the new treatment group. This
translates into a two-year survival rate of 80.1% for the old treatment group
and only 52.9% for the new treatment group. The differ-ence between these two
proportions is clearly significant. So the old treatment is su-perior. Let us
slow down a little and investigate more closely what is going on here. Since we
can split the data into two tables, one for terminal patients and one for
nonterminal patients, it make sense to do this. After all, without treatment
terminal patients are likely to have a shorter survival time than nonterminal
patients. How do these tables compare and what do they show about the
treatments?
Table for Terminal Patients
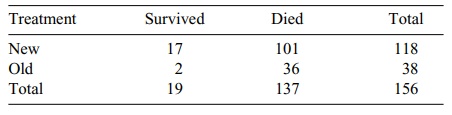
Table for Nonterminal Patients
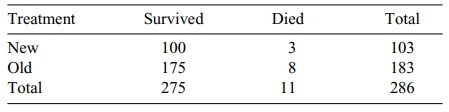
Here we see an entirely different picture! The
survival rate is much lower in the table for terminal patients, as we might
expect. But the new treatment provides a survival rate of 14.4% compared to a
survival rate of only 5.2% for the old treat-ment. For the nonterminal
patients, the new treatment has a 97.1% survival rate compared to a 95.6% rate
for the old treatment. In both cases, the new treatment ap-pears to be better
(the difference between 97.1% and 95.6% may not be statistically significant).
Simpson’s paradox occurs when, as in this example,
two tables each show a higher proportion of success (e.g., survival) for the
one group (e.g., the new treat-ment group), but when the data are combined into
one table the success rate is high-er for the other group (e.g., the old
treatment group). Why did this happen? We have a situation in which the
survival rates are very different for terminal and non-terminal patients but we
did not have uniformity in the number of patients in the ter-minal group that
received the new versus the old treatment. Probably because the new treatment
was expected to help the terminal patients, far more terminal patients were
given the new treatment compared to the old one (118 received the new
treat-ment and only 38 received the old treatment among the terminal patients.
This cre-ated a much larger number of nonsurviving patients in the new
treatment group than in the old treatment group, even though the percentage of
nonsurviving patients was lower. So when the two groups are combined, the new
treatment group is penalized in the overall proportion nonsurviving simply
because of the much higher number of nonsurviving patients contributed by the
terminal group.
So we should not be surprised by the result and the
paradox is not a real one. It does not make sense to pool this data when the
proportions differ so drastically be-tween the classes of patients. Had
randomization been used so that the groups were balanced, we would not see this
phenomenon. Simpson’s paradox is a warning to think carefully about the data
and to avoid combining data into a contingency table when there are known
subgroups with markedly different success proportions. In our example, the
overall survival rate for terminal patients was only 12.2%, with 19 out of 156
surviving. On the other hand, the survival rate for the nonterminal pa-tients
was 96.2%, with 275 out of 286 patients surviving. Although the difference in
proportions is very dramatic here, Simpson’s paradox can occur with differences
that are not as sharp as these. The main ingredient that causes the trouble is
the im-balance in sample sizes between the two treatment groups.
Related Topics
