Limitations to Chi-Square and Exact Alternatives
| Home | | Advanced Mathematics |Chapter: Biostatistics for the Health Sciences: Categorical Data and Chi-Square Tests
The following are some general caveats regarding use of the chi-square test. These guidelines are based on statisticians’ experiences with the test.
LIMITATIONS TO CHI-SQUARE AND EXACT ALTERNATIVES
The following are some general caveats regarding
use of the chi-square test. These guidelines are based on statisticians’
experiences with the test.
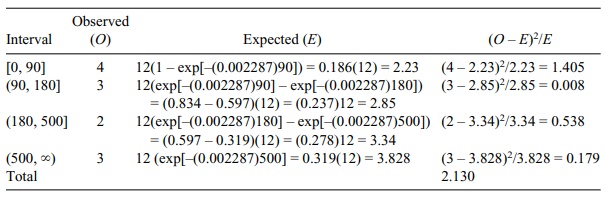
TABLE 11.15. Chi-Square Test for Negative Exponential Distribution
Many statisticians have identified the limitations of the chi-square
test through the use of simulations. As noted, the test should be used for data
in the form of counts, enumerations, or frequencies. A particular cell should
not have small frequencies (e.g., n
< 5), and the grand total N should
be greater than 20. The chi-square test is an approximate test, and the
approximation can be poor when the cell frequencies are low. In a two-way or N-way table, the subjects being
classified should be chosen independently (with the exception of McNemar’s
test). For example, if one is studying sex differ-ences, one should choose
samples of males and females independently.
An example of nonindependent selection would be to
choose men and women who are spouses. Similarly, pairs of twins would not
qualify as independently se-lected. In the special case of a 2 × 2 table,
Yates’ correction gives an improved esti-mation of chi-square. Yates’
correction is built into the calculation formula as N/2 and gives an improved estimate of χ2 when df
= 1.
Given that the chi-square test does not involve
parameter values directly, it does not have a corresponding confidence
interval. Furthermore, it is not easy to calcu-late the required sample sizes
(power testing) for a chi-square test. However, the software package StatXact
5.0, described in Chapter 16, calculates power and sam-ple sizes for the
analogous exact tests. .
Among the alternatives for the 2 × 2 table is
Fisher’s exact test, which Chapter 14 (section on permutation tests) will cover
in detail. We use Fisher’s exact test for problems that involve small sizes
when expected cell values are smaller than 5. This test is based on specifying
that the row and column totals are fixed. Various other exact tests are
described in detail in the StatXact users guide.
Related Topics
