What is radioactivity?

What is radioactivity?

The atomic structure

It is fundamental to look at the structure of an atom in order to understand what radioactivity is. As discussed in Chapter 1 and briefly summarised here, an atom consists of a positively charged nucleus formed from the so-called nucleons, which is surrounded by negatively charged electrons, which may occupy different energy levels. Protons and neutrons form the nucleus. Protons are nucleons with a positive charge and a mass of 1.6726 × 10⁻²⁴ g. The atomic number (Z) expresses the number of protons. A neutron is a nucleon without a charge and a mass similar to that of protons (1.6749 × 10⁻²⁴ g). The so-called neutron number (N) describes the total number of neutrons. Neutrons and protons are held together by nuclear binding forces and therefore form the nucleus. The letter A stands for the number of nucleons, which is the sum of number of protons (Z) and neutrons (N). Electrons have a mass of 9.1094 × 10⁻²⁸ g and they move in energy levels around the nucleus. Lower orbitals, which are defined as the orbitals closer to the nucleus, possess a higher kinetic energy. If an electron moves to an orbital closer to the nucleus, energy is released, whilst the energy is required to move it away from the nucleus. 

The number of electrons should be equal to the number of protons in order to have an element without any charge. Typically, the number of neutrons equals the number of protons (Figure 10.1).

Radioactive processes

Radioactive decay, also known as radioactivity, describes the process by which an unstable nucleus spon-taneously loses energy in order to form a stable nucleus. This energy loss is achieved by emitting particles of ionising radiation. An element or material that spontaneously emits energy in this form is considered as radioactive. Radiation can take place in the form of α, β⁻, β⁺, X-rays and γ-rays.

Radioactivity is defined as the process whereby an unstable nucleus spontaneously loses energy in order to form a more stable nucleus.

The terms nuclide and radionuclide describe identifiable atomic species (nonradioactive or radioactive), which are characterised by their exact number of protons (Z) and neutrons (N). In contrast, an element is only defined by its number of protons (Z). The number of neutrons can vary, which leads to different isotopes of the same element as described in Chapter 1. An element can have a number of isotopes, some of which are stable and some are not stable and therefore are classified as radioactive.

Radioactive decay

It is important to understand the different forms of radioactive decay, as not all forms of radiation are useful for clinical applications. It is also crucial to understand the reason for the occurrence of radioactivity in order to provide the patient with the best and safest possible treatment option.

There are two reasons for the occurrence of radioactive decay: one is that the ratio of neutrons to protons is greater or less than 1. The second reason is that radioactive decay takes places as a result of an energy imbalance within the atom, which means that the atom needs to get rid of energy in order to reach a stable form. The different forms of radiation can be summarised as α, β, γ-decay and X-ray emission.

Alpha-(α-)radiation is defined as the emission of helium particles, precisely ⁴₂He²⁺. α-Decay occurs in elements with a so-called heavy nucleus, principally in elements with a higher atomic mass (typically in ele-ments with Z > 82). α-Particles are fairly heavy particles and follow a straight path when penetrating through a material. They only display a short-range activity and the radiation can be easily shielded off with a piece of paper. 

Their clinical application is very limited and includes only a few therapeutic examples. Current research includes the use of monoclonal antibodies as radiopharmaceuticals. The idea is to deliver radioiso-topes directly to the tumour cells, minimising the exposure of healthy cells to radiation.

In general, interaction of α-radiation with neighbouring matter can occur in two ways – through ionisation or excitation. Excitation means that an α-particle can, upon collision, promote an electron to a higher energy level (higher outer shell). Once the electron falls back to its original energy level, energy is emitted. The more important interaction is the ionisation of an atom. This occurs when an α-particle collides with its target and ‘strips’ away an electron, leaving behind a positively charged molecule (Figure 10.2).

Beta-(β-)decay occurs when basically an electron is ejected from the nucleus. This occurs when the ‘neutron to proton ratio’ is >1. In order for this to happen, within the nucleus a neutron is converted into a proton and a negatively charged β-particle (negatron, β⁻). Additionally a so-called antineutrino ( ) is ‘produced’, carrying away any excess binding energy from the nucleus. These processes result in an increase in the proton number (Z) to Z + 1 and a decrease in the neutron number (N) to N − 1. Negatively charged β-particles have the appearance of electrons, but they originate from the nucleus and carry energy. In contrast, electrons that are present in the orbit outside the nucleus have no energy and obviously their origin differs (Figure 10.3).

β-Particles differ significantly from α-particles as they are considered as extremely light and fast particles. As a consequence, they travel much further and their clinical applications include imaging methods as well as therapeutic ones, with the emphasis being on the latter.

Positron emission is the ejection of positively charged β-particles from a proton-rich nucleus. This occurs when the neutron to proton ratio is <1. For this to happen, a proton is converted into a neutron, a positron (β⁺) and a neutrino (v). A neutrino is the opposite of an antineutrino, a small particle carrying no mass or charge. These processes result in a decrease in the proton number (Z) to Z − 1 and an increase in the neutron number (N) to N + 1. The differences between a positron and a neutron manifest in a lower energy and range for positrons. Positrons and positron-emitting elements are used mainly for imaging purposes in the so-called positron emission tomography (PET, see Chapter 10) (Figure 10.4).

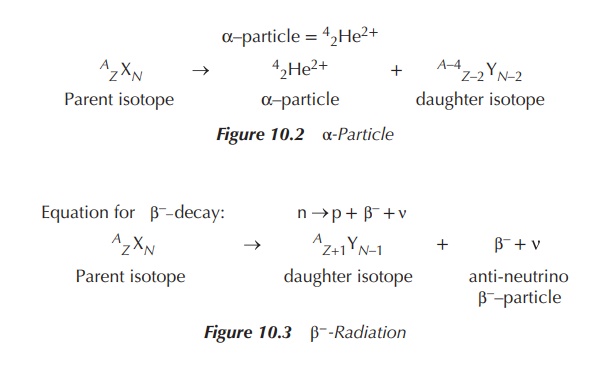
Gamma-(γ-)emission is the elimination of excess energy by the emission of photons. A γ-photon has no charge or mass and occurs as electromagnetic radiation. The radiation occurs at short wavelengths and is therefore of high energy. It has the longest range of all nuclear emissions discussed. The nucleus that emits the γ-photon does not undergo any change of the neutron number; mostly isomers are formed. Isomers are defined as nuclides of the same atomic mass (A) and number (Z) with the only difference being that one isomer is in an excited (metastable (m)) state. This is marked with ^AmE as the atomic number (Figures 10.5 and 10.6).

γ-Emission normally occurs following another nuclear decay. It has a high penetrating power of several metres as the γ-photons are not charged. They typically interact with matter through direct collision with nuclei and electrons of the orbital. γ-Emission finds its clinical application mainly as part of radiopharmaceutical imaging processes.

Electron capture and X-ray emission constitutes another form of positron emission and occurs in unstable atoms where the ‘neutron to proton’ ratio is <1. In order to convert to a stable atom, a proton from the nucleus catches an electron from the orbital and transforms into a neutron and a neutrino, with the neutrino carrying any excess energy. Typically, a cascade reaction follows, in which electrons from the outer (higher energy) orbitals move closer to the nucleus and fill the vacated orbitals. Orbitals closer to the nucleus are of lower energy, and the energy difference is given off as X-rays, a form of electromagnetic radiation. In contrast to γ-decay, which originates predominantly from the nucleus, X-rays stem from outside the nucleus. Additionally, X-rays have a wavelength longer than γ-photons. The result of electron capture and X-rays are the so-called isobars, similar to β-decay.

Isobars are nuclides with the same mass number (A) but different atomic number (Z) and different neutron number (N).

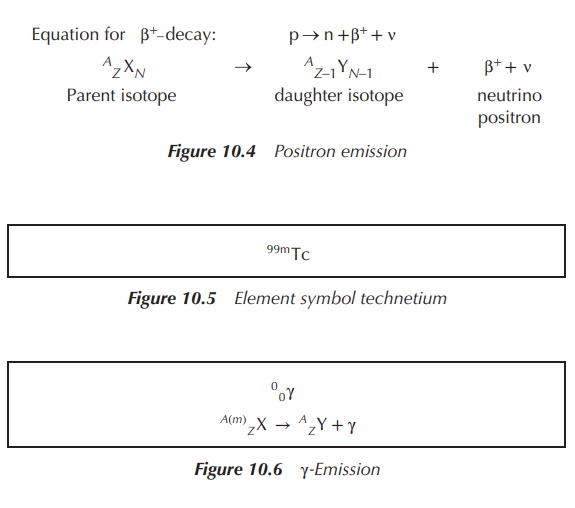
Figure 10.7 shows the effect of charge on different forms of radiation. A radioactive sample is placed in a container, where radiation is released in only one direction. This directed radiation is then exposed to a nega-tively and a positively charged electrode. As a result, the α-particles (positive charged particles) are directed towards the negative charge, whereas the gamma rays are not affected by the charge at all. Consequently, the negatively charged β-particles are directed towards the positive charge.

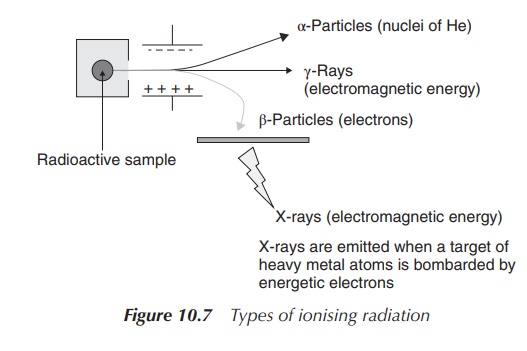
Penetration potential

It is important to understand the different penetration potentials of the various forms of radioactive decay in order to evaluate their clinical potential and the safety concerns of radiopharmaceutical compounds. α-Particles have the shortest range and can be stopped by paper. Skin is typically thick enough to provide sufficient protection. It is dangerous to ingest α-particles as it can cause serious damage to the affected areas. Unfortunately, it is difficult to monitor α-radiation. α-Particles have typically a long half-life and cause cell death, and therefore can sometimes be used in cancer treatment.

β-Particles cause ionisation and excitation (similar to α-particles) when they interact with matter. Inges-tion is also a serious problem, as many β-radioisotopes are isotopes of carbon, hydrogen, sulfur, phosphorus and other essential elements and can easily be incorporated into biological material in the human body. This can lead to extensive damage of DNA and tissue. Additionally, many β-particles have relatively long half-lives. Fortunately, they can be shielded by a few millimetres of aluminium or plastic and are easy to monitor.

γ-Photons also cause ionisation and excitation, but not as successfully as α-particles or β-particles. The energy of γ-photons is usually larger than that of chemical bonds and can destroy biological structures in the human body. Their penetration potential is the highest amongst the types of radiation discussed here. γ-Photons can penetrate through skin and tissue easily. Shielding requires a few inches of lead or a few feet of concrete.

Quantification of radioactivity

Radioactivity can be quantified, and there are several units being used in order to describe the energy, exposure and the dose of radiation. It is crucial for a nuclear pharmacist to understand these units in order to dispense and handle radioactive material correctly.

1. Units of radioactivity

The activity of a radioactive source is defined as the number of transformations per unit time. The old tra-ditional unit of radiation is curie (Ci). One curie is defined as 3.7 × 10¹⁰ disintegrations per second (dps). Nevertheless, the SI unit is becquerel (Bq), which is equal to 1 dps and is a metric unit (Figure 10.8, Tables 10.1 and 10.2).

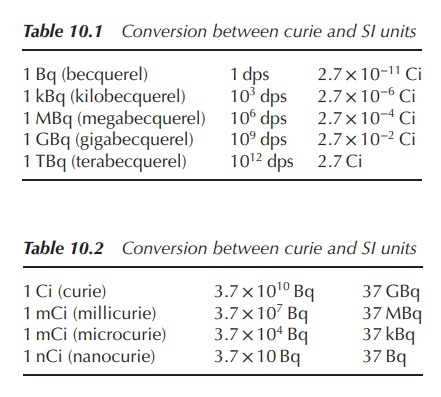
For a pharmacist, it is crucial to know the specific activity of a radioactive preparation. This is the activity of a particular radionuclide per unit mass of this element, usually expressed in grams. The radioactive con-centration of a solution is defined as the activity of a particular radionuclide per unit volume. The absorbed dose is the energy deposited per unit mass of the material. The unit 1 gray (Gy) is equal to 1 J of energy absorbed in 1 kg of material. As a comparison, ∼25 Gy is need to kill bacteria when sterilising. The ‘dose equivalent’ takes also into account variations in the biological effectiveness of different radiation. The unit is sievert (1 Sv) (Figure 10.9).

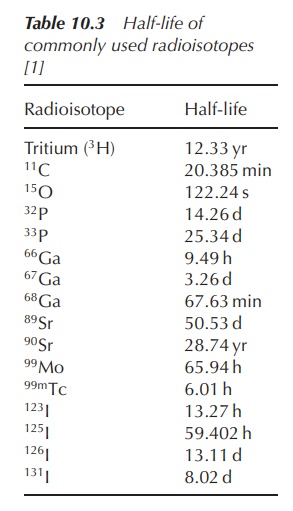
2. Half-life (t_1/2)

For nuclear pharmacists, it is also important to understand the term half-life (t_1/2 ), as this gives information on how fast the radioactive decay takes place. The shorter the half-life, the faster the radioisotope decays. 

The half-life of radioactive elements can vary from several years to less than a second. Typical examples include ¹⁴C (5730 years), ²⁴Na (15 h) and ¹⁸Kr (13 s). Radiopharmaceuticals are typically divided into products with long (>12 h) and short (<12 h) half-lives.

Half-life (t_1/2) is defined as the time it takes for the activity (or the amount of radioactivity) to reduce by 50%. The shorter the half-life, the faster the isotope decays and the more unstable it is. The half-life is unique for any given radioisotope.

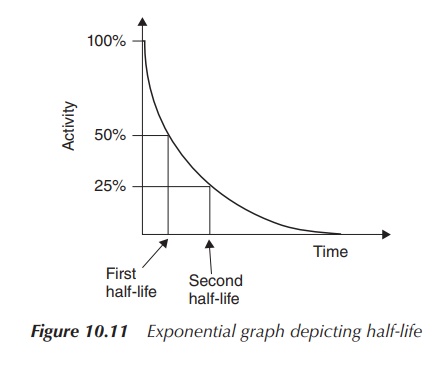
Radioactive decay follows an exponential curve and it is therefore possible to determine the half-life by plotting a graph of activity versus time (see Figure 10.10). The first half-life is the point on the time axis at which only 50% of the initial activity remains. Subsequently, the second half-life is the time point at which the activity has halved again, that is, 25% of the original activity is left (Figure 10.11).

Dose equivalent = Absorbed dose × Quality factor

The quality factor for β- and γ-radiation is 1 and therefore 1 Sv = 1 Gy

Figure 10.10 Dose equivalent

The so-called decay constant λ is related to half-life t_1/2 and can be calculated by using the following formula:

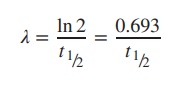
Example

The decay constant for ^99mTc is 0.1153 h⁻¹. Calculate the half-life (t_1/2) of this radioisotope (Table 10.3).

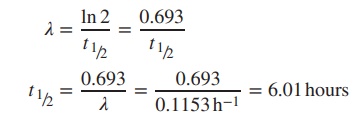
3. Calculation of radioactive decay

It is important for the healthcare professional to predict the activity of the radioactive material at any point in time before or after the assay being undertaken, as it is crucial to know the exact activity at administration to the patient. The radioactive decay can be described as the average number of radioactive isotopes (N) disin-tegrating per unit time (=disintegration rate). The disintegration rate is defined as −dN/dt. The disintegration rate is proportional to the number of undisposed radioisotopes, and can be also expressed as the activity (A).

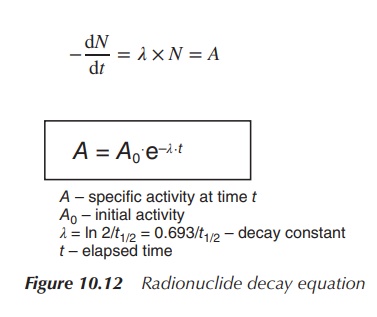
Upon integration, the radioactive decay of any radioactive sample can be calculated by applying the so-called radionuclide decay equation (see Figure 10.12). In order to calculate the radioactivity at a specific time point t, it is important to know the initial activity A₀, the elapsed time t and the decay constant . Half-life is the time that passes by until the activity has halved.

Example

A radioactive sample has a half-life of 8.05 days and contains 150 mCi radioactivity. Calculate the radioac-tivity left after 20 days.

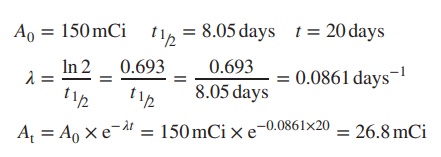
4. Dispensing of radioisotopes: percentage activity and activity concentration

For the dispensing pharmacist, it is crucial to know the activity of a radioactive sample at any given time. The factor e^{− t} from the decay equation A = A₀e^{− t} is called the decay factor and can be used to calculate the percentage activity remaining after given time t. The percentage activity can be calculated using the following equation:

Percentage activity = 100 × e^{− λt}

Example

 ¹³¹I has a half-life of 8.05 days. Calculate the percentage of ¹³¹I remaining after 4.5 days.

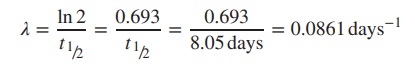
Percentage activity after 4.5 days = 100 × e^{− λt} = 100 × e^{−0.0861×4.5} = 67.88%

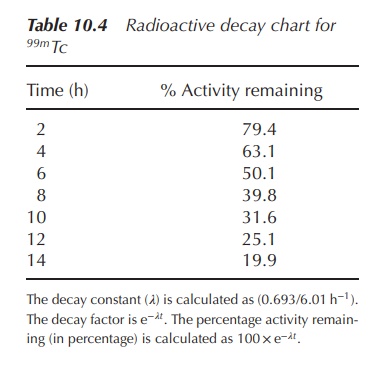
Radioactive decay charts, that is, charts showing the percentage activity at certain time points, are often used in hospitals for quick reference. A representative table illustrating the percentage activity for the radioisotope ^99mTc is shown in Table 10.4.

Radioisotopes are often dispensed according to their specific activity and activity concentration. The specific concentration is defined as the amount of radioactivity, usually expressed in curie, per unit mass. For example, a sample of containing 50 mg of ^99mTc-albumin has an activity of 100 mCi. Therefore, the specific activity can be determined as 100 mCi/50 mg = 2 mCi/mg.

Most radioactive products are dispensed as solutions, and therefore the term activity concentration is important to understand. The activity concentration is defined as the radioactivity expressed in curie, per unit volume. A 5 ml solution of ^99mTc-albumin has a radioactivity of 100 mCi. Therefore, the activity con-centration is 100 mCi/5 ml = 20 mCi/ml. Once the activity concentration is known, the right dose (volume) containing the correct radioactivity can be dispensed.

Quantity(ml) = Activity required / Activity concentration

Example

The current activity concentration of a radiopharmaceutical is 20 mCi/ml. A solution with a dose of 15 mCi has been ordered. What quantity needs to be dispensed in order to provide a sample with the correct radioactivity?

activity concentration ∶ 20 mCi∕ml activity requested ∶ 15 mCi

Quantity needed = 15 mCi∕20 mCi∕ml = 0.75 ml = amount to be dispensed