Free Energy Change

FREE ENERGY CHANGE

The change in free energy is represented in two ways, ∆G and ∆Go. The first, ∆G (without the superscript “o”), represents the change in free energy and, thus, the direction of a reaction at any specified concentration of products and reactants. DG, then, is a variable. This contrasts with the standard free energy change, ∆G^o (with the superscript “o”), which is the energy change when reactants and products are at a concentration of 1 mol/l. [Note: The concentration of protons is assumed to be 10–7 mol/l (that is, pH = 7). This may be shown by a prime sign (I), for example, ΔGoI.] Although ∆Go, a constant, represents energy changes at these nonphysiologic concentrations of reactants and products, it is nonetheless useful in comparing the energy changes of different reactions. Furthermore, ∆G^o can readily be determined from measurement of the equilibrium constant. This section outlines the uses of ∆G, and ∆G^o is described on later section.

A. Sign of ∆G and the direction of a reaction

∆G can be used to predict the direction of a reaction at constant temperature and pressure. Consider the reaction:

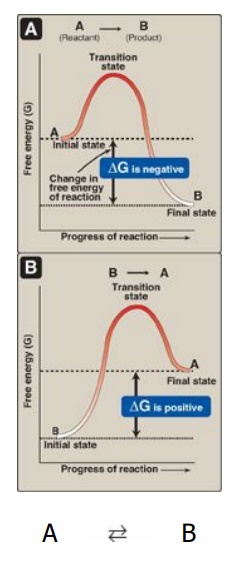
Figure 6.2 Change in free energy (ΔG) during a reaction. A The product has a lower free energy (G) than the reactant. B The product has a higher free energy than the reactant.

A ↔ B

1. Negative ∆G: If ∆G is negative, there is a net loss of energy, and the reaction goes spontaneously as written (that is, A is converted into B) as shown in Figure 6.2A. The reaction is said to be exergonic.

 2. Positive ∆G: If ∆G is positive, there is a net gain of energy, and the reaction does not go spontaneously from B to A (see Figure 6.2B). Energy must be added to the system to make the reaction go from B to A. The reaction is said to be endergonic.

3. ∆G is zero: If ∆G = 0, the reactants are in equilibrium. [Note: When a reaction is proceeding spontaneously (that is, free energy is being lost) then the reaction continues until ∆G reaches zero and equilibrium is established.]

B. ∆G of the forward and back reactions

The free energy of the forward reaction (A → B) is equal in magnitude but opposite in sign to that of the back reaction (B → A). For example, if ∆G of the forward reaction is −5 kcal/mol, then that of the back reaction is +5 kcal/mol. [Note: ∆G can also be expressed in kilojoules per mole or kJ/mol (1 kcal = 4.2 kJ).]

C. ∆G and the concentration of reactants and products

The ∆G of the reaction A → B depends on the concentration of the reactant and product. At constant temperature and pressure, the following relationship can be derived:

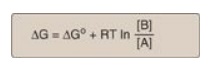
where

where

∆G^o is the standard free energy change (see below)

R is the gas constant (1.987 cal/mol K)

T is the absolute temperature (K)

[A] and [B] are the actual concentrations of the reactant and product

In represents the natural logarithm

A reaction with a positive ∆Go can proceed in the forward direction (have a negative overall ∆G) if the ratio of products to reactants ([B]/[A]) is sufficiently small (that is, the ratio of reactants to products is large). For example, consider the reaction:

Glucose 6-phosphate ↔ fructose 6-phosphate

Figure 6.3A shows reaction conditions in which the concentration of reactant, glucose 6-phosphate, is high compared with the concentration of product, fructose 6-phosphate. This means that the ratio of the product to reactant is small, and RT ln([fructose 6-phosphate]/[glucose 6-phosphate]) is large and negative, causing ∆G to be negative despite ∆Go being positive. Thus, the reaction can proceed in the forward direction.

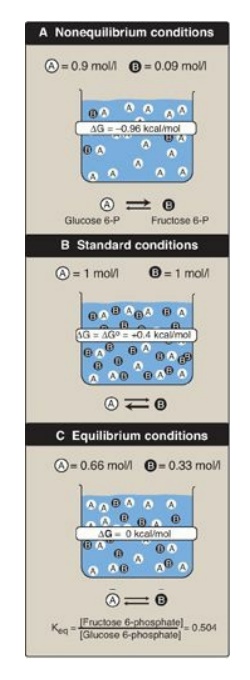
Figure 6.3 Free energy change (  ) of a reaction depends on the concentration of reactant and product . For the conversion of glucose 6-phosphate to fructose 6-phosphate, ΔG is negative when the ratio of reactant  to product  is large (top, panel A), is positive under standard conditions (middle, panel B), and is zero at equilibrium (bottom, panel C). ΔG0 = standard free energy change.

D. Standard free energy change

Τhe standard free energy change, ∆G^o, is so called because it is equal to the free energy change, ∆G, under standard conditions (that is, when reactants and products are at 1 mol/l concentrations; see Figure 6.3B). Under these conditions, the natural logarithm of the ratio of products to reactants is zero (ln1 = 0), and, therefore, the equation shown at the bottom of the previous page becomes:

∆G = ∆G^o + 0

1. ∆G^o and the direction of a reaction: Under standard conditions, ∆G^o can be used to predict the direction a reaction proceeds because, under these conditions, ∆G^o is equal to ∆G. However, ∆G^o cannot predict the direction of a reaction under physiologic conditions, because it is composed solely of constants (R, T, and Keq [see below]) and is not, therefore, altered by changes in product or substrate concentrations.

2. Relationship between ∆G^o and K_eq: In a reaction A ↔ B, a point of equilibrium is reached at which no further net chemical change takes place (that is, when A is being converted to B as fast as B is being converted to A). In this state, the ratio of [B] to [A] is constant, regardless of the actual concentrations of the two compounds:

K_eq = [B]_eq / [A]_eq

where Keq is the equilibrium constant, and [A]_eq and [B]_eq are the concentrations of A and B at equilibrium. If the reaction A ↔ B is allowed to go to equilibrium at constant temperature and pressure, then, at equilibrium, the overall ∆G is zero. Therefore,

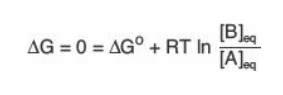
where the actual concentrations of A and B are equal to the equilibrium concentrations of reactant and product [A]_eq and [B]_eq, and their ratio is equal to the K_eq. Thus,

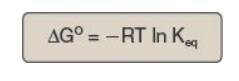
This equation allows some simple predictions:

3. ∆G^o of two consecutive reactions: The ∆G^os are additive in any sequence of consecutive reactions, as are the ∆Gs. For example:

4. ∆Gs of a pathway: The additive property of free energy changes is very important in biochemical pathways through which substrates must pass in a particular direction (for example, A → B → C → D →…). As long as the sum of the ∆Gs of the individual reactions is negative, the pathway can potentially proceed as written, even if some of the individual reactions of the pathway have a positive ∆G. The actual rate of the reactions does, of course, depend on the lowering of activation energies by the enzymes that catalyze the reactions.

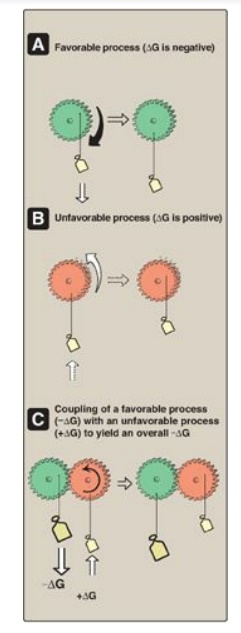
Figure 6.4 Mechanical model of coupling of favorable and unfavorable processes.A Gear with weight attached spontaneously turns in the direction that achieves the lowest energy state. B The reverse movement is energetically unfavorable (not spontaneous). C The energetically favorable movement can drive the unfavorable one.