Michaelis-Menten Kinetics

MICHAELIS-MENTEN KINETICS

A. Reaction model

Leonor Michaelis and Maude Menten proposed a simple model that accounts for most of the features of enzyme-catalyzed reactions. In this model, the enzyme reversibly combines with its substrate to form an ES complex that subsequently yields product, regenerating the free enzyme. The model, involving one substrate molecule, is represented below:

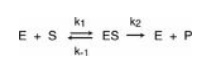
where

S is the substrate

E is the enzyme

ES is the enzyme–substrate complex

P is the product

k₁, k_-1, and k₂ are rate constants

B. Michaelis-Menten equation

The Michaelis-Menten equation describes how reaction velocity varies with substrate concentration:

where

Vo = initial reaction velocity

Vmax = maximal velocity

Km = Michaelis constant = (k_-1 + k₂)/k₁

[S] = substrate concentration

The following assumptions are made in deriving the Michaelis-Menten rate equation:

1. Relative concentrations of enzyme and substrate: The concentration of substrate ([S]) is much greater than the concentration of enzyme ([E]), so that the percentage of total substrate bound by the enzyme at any one time is small.

2. Steady-state assumption: [ES] does not change with time (the steady-state assumption), that is, the rate of formation of ES is equal to that of the breakdown of ES (to E + S and to E + P). In general, an intermediate in a series of reactions is said to be in steady state when its rate of synthesis is equal to its rate of degradation.

3. Initial velocity: Initial reaction velocities (vo) are used in the analysis of enzyme reactions. This means that the rate of the reaction is measured as soon as enzyme and substrate are mixed. At that time, the concentration of product is very small, and, therefore, the rate of the back reaction from product to substrate can be ignored.

C. Important conclusions

1. Characteristics of Km: Km, the Michaelis constant, is characteristic of an enzyme and its particular substrate and reflects the affinity of the enzyme for that substrate. Km is numerically equal to the substrate concentration at which the reaction velocity is equal to 1⁄2 Vmax. Km does not vary with enzyme concentration.

a. Small Km: A numerically small (low) K_m reflects a high affinity of the enzyme for substrate, because a low concentration of substrate is needed to half-saturate the enzyme—that is, to reach a velocity that is 1⁄2 Vmax (Figure 5.9).

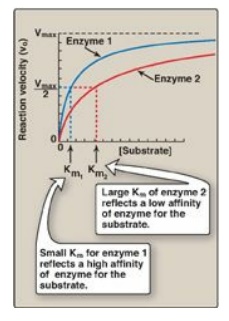
Figure 5.9 Effect of substrate concentration on reaction velocities for two enzymes: enzyme 1 with a small Michaelis constant (Km) and enzyme 2 with a large Km. Vmax = maximal velocity.

b. Large Km: A numerically large (high) K_m reflects a low affinity of enzyme for substrate because a high concentration of substrate is needed to half-saturate the enzyme.

2. Relationship of velocity to enzyme concentration: The rate of the reaction is directly proportional to the enzyme concentration at all substrate concentrations. For example, if the enzyme concentration is halved, the initial rate of the reaction (v_o), as well as that of Vmax, are reduced to half that of the original.

3. Order of reaction: When [S] is much less than Km, the velocity of the reaction is approximately proportional to the substrate concentration (Figure 5.10). The rate of reaction is then said to be first order with respect to substrate. When [S] is much greater than Km, the velocity is constant and equal to Vmax. The rate of reaction is then independent of substrate concentration (the enzyme is saturated with substrate) and is said to be zero order with respect to substrate concentration (see Figure 5.10).

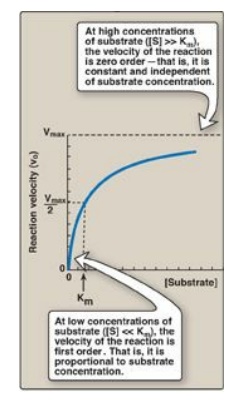
Figure 5.10 Effect of substrate concentration on reaction velocity for an enzymecatalyzed reaction. Vmax = maximal velocity; Km = Michaelis constant.

D. Lineweaver-Burk plot

When v_o is plotted against [S], it is not always possible to determine when V_max has been achieved because of the gradual upward slope of the hyperbolic curve at high substrate concentrations. However, if 1/v_o is plotted versus 1/[S], a straight line is obtained (Figure 5.11). This plot, the Lineweaver-Burk reciprocal plot) can be used to calculate K_m and V_max mechanism of action of enzyme inhibitors.

1. The equation describing the Lineweaver-Burk plot is:

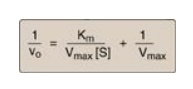
where the intercept on the x axis is equal to −1/K_m, and the intercept on the y axis is equal to 1/V_max. [Note: The slope = K_m/V_max.]

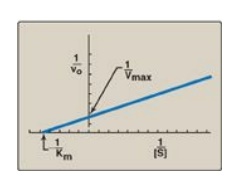
Figure 5.11 Lineweaver-Burk plot. v_o = reaction velocity; V_max = maximal velocity; K_m = Michaelis constant; [S] = substrate concentration.